Cho tam giác ABC , điểm M,N lần lượt là trung điểm của các cạnh AB,AC Hãy tính diện tích tứ giác MNCB?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 9 2017
Xét tam giác ABC có M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC.
Suy ra: MN // BC và
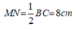
Do đó, tứ giác MNCB là hình thang .
Vì AH = 8cm nên đường cao kẻ từ M đến BC bằng
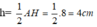
Diện tích hình thang MNCB là :
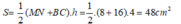
Chọn đáp án A
TM
11 tháng 9 2021
a/ M, N là trung điểm của AB, AC ⇒ MN là đường trung bình của △ABC, MN // BC (1)
Vậy: MNCB là hình thang (đpcm)
==========
b/ Do MN là đường trung bình của △ABC
Vậy: \(MN=\dfrac{BC}{2}\Rightarrow BC=MN.2=3,5.2=7cm\)
==========
c/ Do E là trung điểm của BC \(\Rightarrow CE=\dfrac{BC}{2}\)
- Mà \(MN=\dfrac{BC}{2}\Rightarrow MN=CE\left(2\right)\)
Từ (1) và (2). Vậy: MNCE là hình bình hành (đpcm)
7 tháng 5 2017
a, dt =40 x 50 : 2 = 1000cm2
b, lấy D là trung điểm BC,nối A với D tta được 4 tam giác = nhau
BMD = DMA =ADN= DNC =1/4 ABC
nối M với N ta có MNA = MND và = 1/3 ABC
vậy MNCB=3/4ABC = 1000 : 4 x 3 = 750 cm2
ĐS MNCB = 750 cm2