s= 3/10+3/11+3/12+3/13+3/14 chung minh rang 1<s<2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


* S = 3/10+3/11+3/12+3/13+3/14 < 3/10 + 3/10+3/10+3/10+3/10
< 3/10 x 5
< 3/2 < 2sư
* S = 3/10+3/11+3/12+3/13+3/14 > 3/15+3/15+3/15+3/15+3/15
> 3/15 x 5
> 1
CHỨNG TỎ ........
> 1

3/10=3/9*10
3/11=3/10*11
3/12=3/11*12
3/13=3/12*13
3/14=3/13*14
suy ra 3/10+3/3/11+....+3/14 nhỏ hơn 3/9*10+....+3/13*14
suy ra 3/9*10 + 3/10*11+....+3/13*14
=1/9-1/10+....+1/13-1/14
=1/9-1/14
tự viết kết quả nhé


Ta có: \(S=\frac{3}{10}+\frac{3}{11}+\frac{3}{12}+\frac{3}{14}>\frac{3}{14}+\frac{3}{14}+\frac{3}{14}+\frac{3}{15}=\frac{15}{14}>1\)(1)
\(S=\frac{3}{10}+\frac{3}{11}+\frac{3}{12}+\frac{3}{13}+\frac{3}{14}< \frac{3}{10}+\frac{3}{10}+\frac{3}{10}+\frac{3}{10}+\frac{3}{10}=\frac{15}{20}< 2\)(2)
Từ (1) và (2), suy ra 1 < S < 2. Mà 1 và 2 là hai số tự nhiên liên tiếp. Suy ra S không phải số tự nhiên (đpcm)
Bạn tham khảo nhé
Ta có :
\(S=\frac{3}{10}+\frac{3}{11}+\frac{3}{12}+\frac{3}{13}+\frac{3}{14}>\frac{3}{14}+\frac{3}{14}+\frac{3}{14}+\frac{3}{14}+\frac{3}{14}=\frac{15}{14}>\frac{14}{14}=1\)\(\left(1\right)\)
Lại có :
\(\frac{3}{10}+\frac{3}{11}+\frac{3}{12}+\frac{3}{13}+\frac{3}{14}< \frac{3}{10}+\frac{3}{10}+\frac{3}{10}+\frac{3}{10}+\frac{3}{10}=\frac{15}{10}=\frac{3}{2}=1,5\)\(\left(2\right)\)
Từ (1) và (2) suy ra :
\(1< S< 1,5\)
Vậy S không là số tự nhiên


\(S=\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}\)
\(\Rightarrow S< \dfrac{3}{10}+\dfrac{3}{10}+\dfrac{3}{10}+\dfrac{3}{10}+\dfrac{3}{10}\)
\(\Rightarrow S< \dfrac{15}{10}< 2\)
Lại có \(S>\dfrac{3}{14}+\dfrac{3}{14}+\dfrac{3}{14}+\dfrac{3}{14}+\dfrac{3}{14}\)
\(\Rightarrow S>\dfrac{15}{14}>1\)
\(\Rightarrow1< S< 2\)

Ta có: \(\dfrac{3}{10}>\dfrac{3}{15}\)
\(\dfrac{3}{11}>\dfrac{3}{15}\)
\(\dfrac{3}{12}>\dfrac{3}{15}\)
\(\dfrac{3}{13}>\dfrac{3}{15}\)
\(\dfrac{3}{14}>\dfrac{3}{15}\)
Do đó: \(\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}>\dfrac{3}{15}+\dfrac{3}{15}+\dfrac{3}{15}+\dfrac{3}{15}+\dfrac{3}{15}=1\)
hay 1<S(1)
Ta có: \(\dfrac{3}{11}< \dfrac{3}{10}\)
\(\dfrac{3}{12}< \dfrac{3}{10}\)
\(\dfrac{3}{13}< \dfrac{3}{10}\)
\(\dfrac{3}{14}< \dfrac{3}{10}\)
Do đó: \(\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}< \dfrac{3}{10}+\dfrac{3}{10}+\dfrac{3}{10}+\dfrac{3}{10}=\dfrac{12}{10}\)
\(\Leftrightarrow S< \dfrac{15}{10}=\dfrac{3}{2}< 2\)(2)
Từ (1) và (2) suy ra 1<S<2(đpcm)

\(S=\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}\)
Ta thấy:
\(\dfrac{3}{10}>\dfrac{3}{15}\\\dfrac{3}{11}>\dfrac{3}{15}\\ \dfrac{3}{12}>\dfrac{3}{15}\\ \dfrac{3}{13}>\dfrac{3}{15}\\ \dfrac{3}{14}>\dfrac{3}{15} \)
\(\Rightarrow S=\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}>5\cdot\dfrac{3}{15}\\ S=\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}>1\left(1\right)\)
Mặt khác:
\(\dfrac{3}{10}< \dfrac{3}{9}\\ \dfrac{3}{11}< \dfrac{3}{9}\\ \dfrac{3}{12}< \dfrac{3}{9}\\ \dfrac{3}{13}< \dfrac{3}{9}\\ \dfrac{3}{14}>\dfrac{3}{9}\)
\(\Rightarrow S=\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}< 5\cdot\dfrac{3}{9}\\ S=\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}< \dfrac{5}{3}< 2\left(2\right)\)
Từ (1) và (2) ta có: \(1< S< 2\)

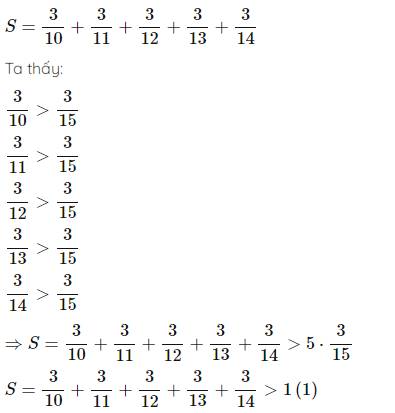
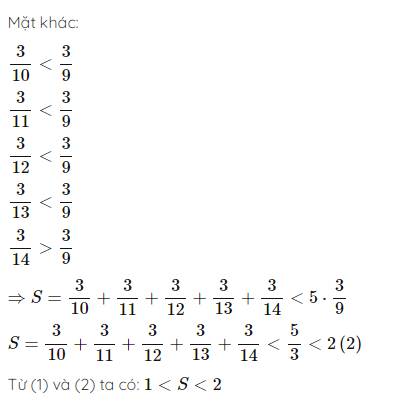
Từ (1) và (2) => 1 < S < 2 (điều phải chứng minh)