Cho các số thực dương \(a;b;c\). Chứng minh rằng :\(\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}\ge4.\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán hỗ trợ, giúp đỡ em bài toán trong đề cương với ạ!Em cám ơn rất nhiều...
Đọc tiếp
Cho các số thực dương \(a;b;c\). Chứng minh rằng :
\(\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}\ge4.\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán hỗ trợ, giúp đỡ em bài toán trong đề cương với ạ!
Em cám ơn rất nhiều ạ!
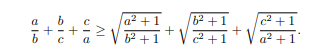
\(S=\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}\)
\(S=\dfrac{b}{a}+\dfrac{c}{a}+\dfrac{c}{b}+\dfrac{a}{b}+\dfrac{a}{c}+\dfrac{b}{c}=a\left(\dfrac{1}{b}+\dfrac{1}{c}\right)+b\left(\dfrac{1}{a}+\dfrac{1}{c}\right)+c\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\ge a.\dfrac{4}{b+c}+b.\dfrac{4}{a+c}+c.\dfrac{4}{a+b}=4\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
Dạ vâng ạ, em chiều nay cũng vừa nghĩ ra được cách này.
Em cám ơn nhiều lắm ạ!