Viết phương trình tham số và phương trình chính tắc của đường thẳng (d): x + y - 20 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đường thẳng d có ![]() và đi qua điểm M(-1; 2)
và đi qua điểm M(-1; 2)
Vậy phương trình tham số của đường thẳng 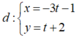 .
.
Chọn C.

∆ ⊥ ( α ) ⇒ a ∆ → = a α → = (2; −1; 1)
Phương trình tham số của ∆ là
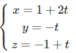
Phương trình chính tắc của ∆ là:
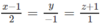

Đường thẳng Δ song song với d ⇒ Δ: x + y + c = 0, (c ≠ 0)
Vì Δ đi qua A ⇒ 3 + 0 + c = 0 ⇒ c = -3(tm)
Vậy đường thẳng Δ có dạng: x+y-3=0
Vì đường tròn có tâm I thuộc d nên I(a;-a)
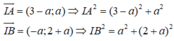
Vì đường tròn đi qua A, B nên I A 2 = I B 2 ⇒ (3 - a ) 2 + a 2 = a 2 + (2 + a ) 2 ⇔ (3 - a ) 2 = (2 + a ) 2
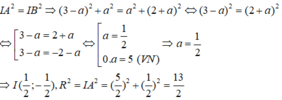
Vậy phương trình đường tròn có dạng:
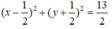
Ta có:
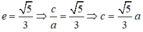
Giả sử elip (E) có dạng:
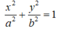
Vì (E) đi qua B nên:
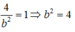
Mà
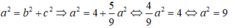
Vậy phương trình chính tắc của elip (E) là:
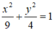

∆ đi qua hai điểm C và D nên có vecto chỉ phương CD → = (1; 2; 3)
Vậy phương trình tham số của ∆ là
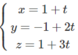
Phương trình chính tắc của ∆ là:
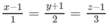

Chọn B.
Đường thẳng d đi qua điểm A(2;0;-1) và có vectơ chỉ phương ![]()
Vậy phương trình chính tắc của d là x - 2 1 = y - 3 = z + 1 5

Chọn B.
Đường thẳng d đi qua điểm A(2;0;-1) và có vectơ chỉ phương ![]()
Vậy phương trình chính tắc của d là x - 2 1 = y - 3 = z + 1 5

Phương trình tham số của đường thẳng Δ đi qua điểm A(1; 2; 3) và có vecto chỉ phương
a
→
= (3; 3; 1) là: 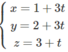
Phương trình chính tắc của ∆ là:
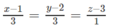
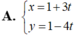

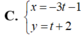
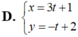


\(\left(d\right):x+y-20=0.\\ \Rightarrow\overrightarrow{n_d}=\left(1;1\right).\\ \Rightarrow\overrightarrow{u_d}=\left(1;-1\right).\)
\(Cho\) \(x=1.\Rightarrow y=19.\Rightarrow A\left(1;19\right)\in\left(d\right).\)
Ta có \(\left(d\right):\) đi qua \(A\left(1;19\right);\overrightarrow{u_d=}\left(1;-1\right)\) là vecto chỉ phương.
\(\Rightarrow\) Phương trình tham số:
\(\left\{{}\begin{matrix}y=1+t.\\y=19-t.\end{matrix}\right.\)
\(\Rightarrow\) Phương trình chính tắc:
\(\dfrac{x-1}{1}=\dfrac{y-19}{-1}.\\ \Leftrightarrow x-1=-y+19.\)
đúng đó