Cho tam giác ABC có A^=1000, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm K sao cho MK = MA. Tính số đo góc ABK^.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

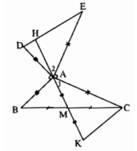
Xét ΔAMB và ΔKMC có:
AM = MK (giả thiết)
BM = MC (vì M là trung điểm của BC)
∠AMB = ∠KMC (hai góc đối đỉnh)
⇒ ΔAMB = ΔKMC (c.g.c)
⇒ ∠ABM = ∠KCM (hai góc t.ư) và AB = CK
⇒ CK // AB (có cặp góc so le trong bằng nhau
+ Ta có: ∠BAM + ∠CAM = 110º ⇒ ∠AKC + ∠CAM = 110º (1)
Xét tam giác ACK có:
∠AKC + ∠CAM + ∠ACK = 180º ( tổng ba góc trong một tam giác). (2)
Từ (1) và (2) suy ra: ∠ACK = 180º - 110º = 70º

a: \(\widehat{ABK}=180^0-100^0=80^0\)
b: Xét tứ giác ABKC có
M là trung điểm của AK
M là trung điểm của BC
Do đó: ABKC là hình bình hành
Suy ra: AC=BK; AB=CK
Xét ΔABK và ΔDAE có
AB=DA
BK=AE
\(\widehat{ABK}=\widehat{DAE}\)
Do đó: ΔABK=ΔDAE

a) Xét ΔACM và Δ KBM có:
MB = MM (gt)
MK = MA (gt)
AMC = BMK (đối đỉnh) => ΔACM = ΔKBM (cgc) => ACM = KBM ( 2 góc tg ứng)
Mà trong tam giác ABC có: A+B+C = 180*=> B+C =80*
=> KBM+ ABC =80*