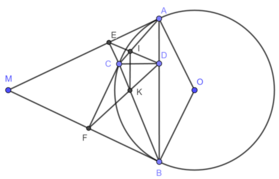
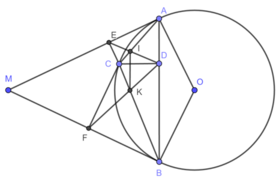
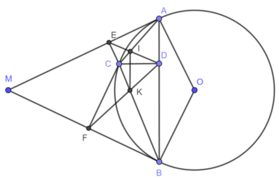
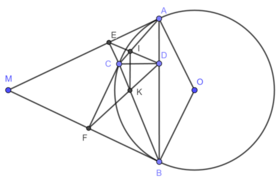
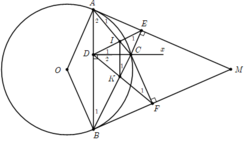
Từ điểm $M$ nằm ngoài đường tròn $(O)$ vẽ hai tiếp tuyến $MA$ và $MB$ với đường tròn đó. Trên cung nhỏ $AB$ lấy điểm $C$. Vẽ \(CD\perp AB\), \(CE\perp MA\), \(CF\perp MB\). Gọi $I$ là giao điểm của $AC$ và $DE$, $K$ là giao điểm của $BC$ và $DF$. Chứng minh rằng :
a) Tứ giác $AECD$, $BFCD$ nội tiếp được.
b) $CD^2 = CE.CF$.
c) \(IK\perp CD\).