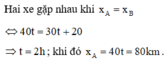Bài 1:Hai xe đạp A và B xuất phát từ một địa điểm và chạy cùng chiều trên một đường đua tròn có chu vi 1,5km.Vận tốc của xe A là 40,5km/h

ND

Natsu Dragneel

20 tháng 6 2016 - olm

Bài 1:Hai xe đạp A và B xuất phát từ một địa điểm và chạy cùng chiều trên một đường đua tròn có chu vi 1,5km.Vận tốc của xe A là 40,5km/h;vận tốc của xe B là 50km/h.Sau khi xe A xuất phát 3 phút thì xe B mới bắt đầu chạy.Hỏi sau bao lâu thì xe B đuổi kịp xe A? Bài 2:Cho hình thang vuông ABCD(vuông tại A và D)có diện tích bằng 24cm2 , có AB bằng 1/3 cạnh CD.Kéo dài DA và CB cắt nhau tại M.Tính...

Đọc tiếp

#Toán lớp 5

0

VP

Vũ Phương Mai

20 tháng 6 2016 - olm

Hai xe máy A và B xuất phát cùng một điểm và chạy cùng chiều và chạy cùng chiều trên một đường đua tròn có chu vi 1 km.Biết vận tốc của xe A là 22,5 km\h, vận tốc của xe là 25 km\h.Sau khi xe A xuất phát được 6 phút thì xe B mới bắt đầu chạy.Hỏi để đuối kịp xe A thì xe B phải chạy trong bao nhiêu phút?

#Toán lớp 5

0

HH

Hoàng Huyền

25 tháng 3 2018 - olm

Hai xe máy A và B xuất phát cùng một điểm và chạy cùng chiều trên một đường đua tròn có chu vi 1km . Biết vận tốc của xe A là 22,5 km/h , vân tốc của xe B là 25km/h . Sau khi xe A xuất phát được 6 phút thì xe B mới bắt đầu chạy . Hỏi để đuổi kịp xe A thì xe B phải chạy trong bao nhiêu phút

#Toán lớp 5

1

LT

Lê Tùng Lâm

27 tháng 1 2021

sao lại 6 p 0,19 mà

Đúng(0)

HH

Hoàng Huyền Trang

29 tháng 7 2017 - olm

hai xe máy A và B chạy cùng chiều trên một quãng đường tròn có chu vi là 1 km vận tốc của xe A là 22,5 km/h vận tốc xe B là 25 km/h sau khi xe A xuất phát được 6 phút thì xe B mới bắt đầu chạy hỏi sau bao lâu thì xe B đuổi kịp xe A

#Toán lớp 5

8

OT

o0o Thúy Loan o0o

30 tháng 7 2017

Đổi 6 phút = 0,1 giờ

Khi xe B xuất phát thì xe A đã chạy được là

22,5 x 0,1 = 2,25 ( km )

Đường đua tròn có chu vi 1 km là

2,25 km = 2 km + 0,25 km

Ta có :

Ta có: 2km + 0,25km . Tức là 2 vòng và 0,25km

Khi xe B xuất phát thì khoảng cách giữa hai xe là: 0,25km.

Hiệu vận tốc của hai xe là:

25 – 22,5 2,5(km/giờ)

Thời gian để xe B đuổi kịp xe A là:

0,25 : 2,5 = 0,19 (giờ)

Đổi: 0,1 giờ = 6 phút

Đáp số : 6 phút

Đúng(0)

SS

Songoku saiyan 4

31 tháng 7 2017

6 phút nhé

Đúng(0)

NT

Nguyễn Thị Hồng Loan

13 tháng 5 2016 - olm

2 xe A và B chạy đua nhau trên 1 vòng tròn cùng xuất phát 1 địa điểm .V xe A=22,5km/h,V xe B=25km/h.Biết xe A xuất phát trước xe B 6 phút.Chu vi đường tròn là 1km.hỏi sau bao nhiêu thời gian xe B gặp xe A?

#Toán lớp 5

0

AD

Anh Đức

5 tháng 9 2021

Hai ôtô chuyển động thẳng đều xuất phát cùng một lúc từ hai điểm A và B trên một đường thẳng cách nhau 20km. Xe 1 xuất phát từ A chạy về B, xe 2 xuất phát từ B chạy cùng chiều xe 1. Vận tốc xe 1 là 50 km/h, xe 2 là 30 km/h. Hỏi sau bao lâu xe 1 gặp xe 2?Tính quãng đường mỗi xe đi được khi gặp nhau và vẽ đồ thị (x-t) của hai...

Đọc tiếp

#Vật lý lớp 10

1

TK

trương khoa

5 tháng 9 2021

Chọn gốc tọa độ O trùng A

Chọn chiều dương trục Ox: từ A đến B

Phương trình chuyển động mỗi xe

\(x_A=50t\left(km,h\right)\)

\(x_B=20+30t\left(km,h\right)\)

Khi 2 xe gặp nhau:

\(x_A=x_B\Rightarrow50t=20+30t\Leftrightarrow t=1\left(h\right)\)

Vậy sau 1 h thì 2 xe gặp nhau và quãng đường mà xe 1 là\(50\cdot1=50\left(km\right)\) và xe 2 là \(30\cdot1=30\left(km\right)\)

< đồ thị bạn tự vẽ nha>;-;

Đúng(1)

DB

Diep Bui Thi

31 tháng 7 2017 - olm

Hai xe máy chạy cùng chiều trên 1 đường đua tròn có chu vi là 1 km. Vận tốc xe A là 22.5 km/giờ, vận tốc xe B là 25 km/giờ. Sau khi xe A xuất phát dc 6 phút thì xe B mới bắt đầu chạy. Hỏi sau bao lâu xe A đuổi kịp xe B?

#Toán lớp 6

1

B1

Ben 10

31 tháng 7 2017

giải theo bài này

gần giống thui

Bài 1:Hai xe đạp A và B xuất phát từ một địa điểm và chạy cùng chiều trên một đường đua tròn có chu vi 1,5km.Vận tốc của xe A là 40,5km/h;vận tốc của xe B là 50km/h.Sau khi xe A xuất phát 3 phút thì xe B mới bắt đầu chạy.Hỏi sau bao lâu thì xe B đuổi kịp xe A?

Bài làm

Sau 3 phút xe A chạy được:

40,5 km/h x 3 phút = 40,5 x 1/20 h = 2,025 km

Mỗi giờ xe B chạy nhanh hơn xe A là:

50km/h - 40,5 km/h= 9,5 km

=> Mỗi phút B nhanh hơn A là:

9,5 km /60 phút = 0,16 km

Vậy sau: 2,025 : 0,16 = 12,78 phút thì B đuổi kịp A

ráng làm đi

Đúng(0)

NQ

Nguyễn Quế Đức

29 tháng 7 2021

Trên một đường đua hình tròn có chu vi l=1000m có hai vận động viên xuất phát đồng thời cùng một vị trí đi xe đạp cùng chiều nhau với vận tốc v1=6m/s và v2=10m/s.a. Tính thời gian từ khi xuất phát đến khi gặp nhau lần thứ nhấtb. Tính khoảng thời gian nhỏ nhất từ khi xuất phát tới khi họ gặp nhau tại chính nơi xuất phát...

Đọc tiếp

#Vật lý lớp 7

1

A

Aurora

30 tháng 7 2021

a. thời gian từ khi xuất phát đến khi gặp nhau lần thứ nhất là \(t=\dfrac{l}{v_2-v_1}=\dfrac{1000}{4}=250\left(s\right)\)

b,thời gian để mỗi xe chạy được một vòng là \(\left\{{}\begin{matrix}t_1=\dfrac{l}{v_1}=\dfrac{1000}{6}=\dfrac{500}{3}\left(s\right)\\t_2=\dfrac{l}{v_2}=\dfrac{1000}{10}=100\left(s\right)\end{matrix}\right.\)

Giả sử lần đầu tiên gặp nhau tại chính nơi xuất phát đó là A

, xe 1 đi thêm x vòng , xe 2 đi thêm y vòng , thời gian mất \(\Delta t\)

ta có \(\Delta t=x.t_1=y.t_2\Leftrightarrow\dfrac{t_1}{t_2}=\dfrac{y}{x}\Leftrightarrow\dfrac{y}{x}=\dfrac{\dfrac{500}{3}}{100}=\dfrac{5}{3}\)

\(\Leftrightarrow\dfrac{y}{x}=\dfrac{5k}{3k}\Leftrightarrow\Delta t=x.t_1=3k.t_1\Rightarrow\Delta t_{min}\Leftrightarrow k=1\)

\(\Rightarrow\Delta t_{min}=3.t_1=500\left(s\right)\)

Đúng(1)

HD

Hoàng Đức Long

27 tháng 7 2018

Cùng một lúc tại hai điểm A và B cách nhau 20 km có hai ô tô chạy cùng chiều nhau trên đường thẳng từ A đến B. Vận tốc của ô tô chạy từ A là 40 km/h và của ô tô chạy từ B là 30 km/h. Chọn A làm mốc, chọn thời điểm xuất phát của hai xe ô tô làm mốc thời gian và chọn chiều chuyển động của hai xe làm chiều dương. Hỏi khoảng thời gian từ lúc hai ô tô xuất phát đến lúc ô tô A đuổi...

Đọc tiếp

#Vật lý lớp 10