cho E= x6 - 6x5 + 6x4 - 6x3 + 6x + 6
tính giá trị của biểu thức E với x=5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P\left(x\right)=5^6-6.5^5+6.5^4-6.5^3+6.5^2-6.5+1=5^6-6\left(5^5-5^4-5^3-5^2-5\right)+1=1556\)

46:
\(A=\dfrac{2x^2\left(3x^2-2x+1\right)}{2x^2}-\left(3x^2-x-6x+2\right)\)
\(=3x^2-2x+1-3x^2+7x-2=5x-1\)
Khi x=-0,2 thì A=-1-1=-2
45:
a: \(=\dfrac{-5x^6}{3x^2}=-\dfrac{5}{3}x^4\)
c: \(=\dfrac{2x\left(2x^2-\dfrac{3}{2}x+1\right)}{2x}=2x^2-\dfrac{3}{2}x+1\)

\(a,n^3-2n^2+3n+3=n^3-n^2-n^2+n+2n-2+5\\ =\left(n-1\right)\left(n^2-n+2\right)+5\\ \Leftrightarrow n^3-2n^2+3n+3⋮\left(n-1\right)\\ \Leftrightarrow5⋮n-1\\ \Leftrightarrow n-1\in\left\{-5;-1;1;5\right\}\\ \Leftrightarrow n\in\left\{-4;0;2;6\right\}\)
\(b,\Leftrightarrow x^4+6x^3+7x^2-6x+a\\ =x^4+3x^3-x^2+3x^3+9x^2-3x-x^2-3x+1-1+a\\ =\left(x^2+3x-1\right)\left(x^2+3x-1\right)-1+a\\ =\left(x^2+3x-1\right)^2+a-1\)
Để \(x^4+6x^3+7x^2-6x+a⋮x^2+3x-1\)
\(\Leftrightarrow a-1=0\Leftrightarrow a=1\)

Biểu thức xác định khi x 2 - 36 ≠ 0 , x 2 + 6 x ≠ 0 , 6 – x ≠ 0 và 2x – 6 ≠ 0
x 2 - 36 ≠ 0 ⇒ (x – 6)(x + 6) ≠ 0 ⇒ x ≠ 6 và x ≠ -6
x 2 + 6 x ≠ 0 ⇒ x(x + 6) ≠ 0 ⇒ x ≠ 0 và x ≠ -6
6 – x ≠ 0 ⇒ x ≠ 6
2x – 6 ≠ 0 ⇒ x ≠ 3
Vậy x ≠ 0, x ≠ 3, x ≠ 6 và x ≠ -6 thì biểu thức xác định.
Ta có:
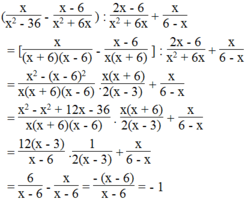
Vậy biểu thức không phụ thuộc vào biến x.

\(E=x^2+6x+11\)
\(=x^2+6x+9+2\)
\(=\left(x+3\right)^2+2>0\forall x\)
\(F=x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\)

a) Tìm được x ≠ -6 và x ≠ 0.
b) Gợi ý: x 3 + 4 x 2 - 6x + 36 = (x + 6) ( x 2 - 2x + 6)
Tìm được P = x 2 − 2 x + 6 2 x
c) Ta có P = 3 2 ⇔ x 2 − 5 x + 6 = 0 . Từ đó tìm được x = 2 hoặc x = 3 (TMĐK).
d) Tương tự câu c, tìm được x = -6 (KTM) hoặc x = -1 (TM)
e) P = 1 Þ x 2 ‑ - 4x + 6= 0 Û ( x - 2 ) 2 + 2 = 0 (vô nghiệm)
Vì ( x - 2 ) 2 + 2 ≥ 2 > 0 với mọi x. Do vậy x ∈ ∅ .

a, a x 6 = 3 x 6 = 18
b, a + b = 4 + 2 = 6
c, b + a = 2 + 4 = 6
d, a - b = 8 - 5 = 3
e, m x n = 5 x 9 = 45