Giải ptr sau: 1/x+2+5/x-2=2x-12/x^2-4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LL
10 tháng 5 2020
\(\left(x+1\right)\left(x+2\right)\left(x+4\right)\left(x+5\right)=40\)
\(\Leftrightarrow\left(x+1\right)\left(x+5\right)\left(x+2\right)\left(x+4\right)=40\)
\(\Leftrightarrow\left(x^2+6x+5\right)\left(x^2+6x+8\right)=40\)
\(\Leftrightarrow\left(x^2+6x+5\right)\left(x^2+6x+5+3\right)=40\)
\(\Leftrightarrow p\left(p+3\right)=40\) (khi đặt \(\left(x^2+6x+5\right)=p\)
\(\Leftrightarrow p^2+3p=40\)
\(\Leftrightarrow p^2\cdot2\cdot p\cdot\frac{3}{2}+\left(\frac{3}{2}\right)^2=\frac{169}{4}\)
\(\Leftrightarrow\left(p+\frac{3}{2}\right)^2-\left(\frac{13}{2}\right)^2=0\)
\(\Leftrightarrow\left(p+\frac{3}{2}-\frac{13}{2}\right)\left(p+\frac{3}{2}+\frac{13}{2}\right)=0\)
\(\Leftrightarrow\left(p-5\right)\left(p+8\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}p=5\\p=-8\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+6x+5=5\\x^2+6x+5=-8\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+6x=0\\x^2+2\cdot x\cdot3+9-9+5=-8\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x\left(x+6\right)=0\\\left(x+3\right)^2=-4\left(\text{vôlí}\right)\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=-6\end{cases}}\)
LL
10 tháng 5 2020
\(\left(x-2\right)\left(x^2+5x-7\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=2\\x^2+5x-7=0\end{cases}}\)
Ta có: \(\Delta=25-4\cdot\left(-7\right)=25+28=53\)
\(\Rightarrow\Delta>0\)
\(\Rightarrow\text{pt có 2 nghiệm pb}\)
\(\Rightarrow\hept{\begin{cases}x_1=\frac{-5-\sqrt{53}}{2}\\x_2=\frac{-5+\sqrt{53}}{2}\end{cases}}\)
\(\text{Vậy pt trên có nghiệm là x=2; x=}\frac{-5\pm\sqrt{53}}{2}\)
22 tháng 4 2021
a) ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
Ta có: \(\dfrac{x+1}{x-2}-\dfrac{5}{x+2}=\dfrac{12}{x^2-4}+1\)
\(\Leftrightarrow\dfrac{\left(x+1\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{5\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{12}{\left(x-2\right)\left(x+2\right)}+\dfrac{x^2-4}{\left(x-2\right)\left(x+2\right)}\)
Suy ra: \(x^2+3x+2-5x+10=12+x^2-4\)
\(\Leftrightarrow x^2-2x+12-8-x^2=0\)
\(\Leftrightarrow-2x+4=0\)
\(\Leftrightarrow-2x=-4\)
hay x=2(loại)
Vậy: \(S=\varnothing\)
22 tháng 4 2021
b) Ta có: \(\left|2x+6\right|-x=3\)
\(\Leftrightarrow\left|2x+6\right|=x+3\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+6=x+3\left(x\ge-3\right)\\-2x-6=x+3\left(x< -3\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-x=3-6\\-2x-x=3+6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\left(nhận\right)\\x=-3\left(loại\right)\end{matrix}\right.\)
Vậy: S={-3}
CC
7 tháng 4 2018
a)\(\sqrt{x^2+x-2}+\sqrt{x^2+2x-3}=\sqrt{x^2+4x-5}\left(1\right)\)
ĐK: \(\left[{}\begin{matrix}x\le-5\\x\ge1\end{matrix}\right.\left(a\right)}\)
Với x = 1 (1) đúng nên x = 1 là 1 nghiệm của (1)
Với \(x\ne1\) chia cả 2 vế của (1) cho \(\sqrt{x-1}\):
\(\left(1\right)\Leftrightarrow\sqrt{x+2}+\sqrt{x+3}=\sqrt{x+5}\left(2\right)\)
ĐK: \(x\ge-5\)
Kết hợp với ĐK(a) =>\(x\ge1\left(b\right)\)
\(\left(2\right)\Leftrightarrow x+2+x+3+2\sqrt{\left(x+2\right)\left(x+3\right)}=x+5\\ \Leftrightarrow x+2\sqrt{\left(x+2\right)\left(x+3\right)}=0\\ \Leftrightarrow2\sqrt{\left(x+2\right)\left(x+3\right)}=-x\)
=>\(x\le0\)
Kết hợp với đk(b)=> không có \(x\ne1\) thỏa mãn pt(1)
Vậy phương trình có nghiệm duy nhất là x=1
21 tháng 3 2021
\(\dfrac{1}{x+2}\)+\(\dfrac{5}{x-2}\)=\(\dfrac{2x-12}{x^2-4}\)
(đkxđ: x≠2, x≠-2)
⇔ \(\dfrac{x-2}{x^2-4}\)+\(\dfrac{5\left(x+2\right)}{x^2-4}\)= \(\dfrac{2x-12}{x^2-4}\)
⇔ x-2+5(x+2)=2x-12
⇔ x-2+5x+10=2x-12
⇔ 4x=-20
⇔ x=-5(tm)
Y
17 tháng 1 2023
\(1,\left(dk:x\ne0,-1,4\right)\)
\(\Leftrightarrow\dfrac{9}{x+1}+\dfrac{2}{x-4}-\dfrac{11}{x}=0\)
\(\Leftrightarrow\dfrac{9x\left(x-4\right)+2x\left(x+1\right)-11\left(x+1\right)\left(x-4\right)}{x\left(x+1\right)\left(x-4\right)}=0\)
\(\Leftrightarrow9x^2-36x+2x^2+2x-11x^2+44x-11x+44=0\)
\(\Leftrightarrow-x=-44\)
\(\Leftrightarrow x=44\left(tm\right)\)
\(2,\left(đk:x\ne4\right)\)
\(\Leftrightarrow\dfrac{14}{3\left(x-4\right)}-\dfrac{2+x}{x-4}-\dfrac{3}{2\left(x-4\right)}+\dfrac{5}{6}=0\)
\(\Leftrightarrow\dfrac{14.2-6\left(2+x\right)-3.3+5\left(x-4\right)}{6\left(x-4\right)}=0\)
\(\Leftrightarrow28-12-6x-9+5x-20=0\)
\(\Leftrightarrow-x=13\)
\(\Leftrightarrow x=-13\left(tm\right)\)
Y
12 tháng 4 2022
\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
Y
12 tháng 4 2022
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)
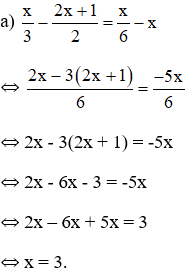
ĐKXĐ: \(x\ne2;x\ne-2\)
\(\Rightarrow x-2+5\left(x+2\right)=2x-12\Leftrightarrow x-2+5x+10=2x-12\Leftrightarrow6x+8-2x=-12\Leftrightarrow4x+8=-12\Leftrightarrow4x=-20\Leftrightarrow x=-5\left(TM\right)\)
ĐKXĐ: \(x\ne\pm2\)
\(\dfrac{1}{x+2}+\dfrac{5}{x-2}=\dfrac{2x-12}{x^2-4}\)
\(\Leftrightarrow\dfrac{x-2}{\left(x+2\right)\left(x-2\right)}+\dfrac{5\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{2x-12}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow x-2+5x+10=2x-12\)
\(\Leftrightarrow2x-12-x+2-5x-10=0\)
\(\Leftrightarrow-4x-20=0\)
\(\Leftrightarrow-4\left(x+5\right)=0\)
\(\Leftrightarrow x+5=0\)
\(\Leftrightarrow x=-5\)
Vậy...