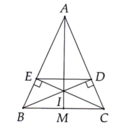
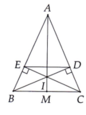
Cho tam giác ABC cân tại A. Vẽ BD vuông với AC tại D, CE vuông với AB tại E . Gọi H là giao điểm của BD và CE. Chứng minh rằng: a) BD = CE b) IH vuông góc BC .giúp mik với ạ 😩🥺❤️❤️
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(g là góc)
Xét tg ABC,có:
AB=AC
=>tg ABC cân tại A
=>gABC = gACB
a)Xét tg BEC và tg CDB ,có:
BC:chung
gBEC =gCDB =90*(vì EC vuông gAB,BD vuông gAC)
gEBC = gDCB(cmt)
=>tg BEC = tg CDB(ch-gn)
=>BD=EC
b)Theo phần a,ta có:tg BEC = tg CDB(ch-gn)
=>gDBC=gECB(2 góc tương ứng)
=>tg BIC cân tại I
=>BI=CI
mà EI+IC=EC và DI+BI=BD(vì I là gđ của BD và EC) và BD=EC(theo phần a)
=>EI = DI
c)Xét tg ABC ,có:
AB=AC(gt)
BI=CI(cmt)
BH=CH(vì H là trung điểm của BC)
=>Ba điểm A, I, H thẳng hàng
(g là góc)
Xét tg ABC,có:
AB=AC
=>tg ABC cân tại A
=>gABC = gACB
a)Xét tg BEC và tg CDB ,có:
BC:chung
gBEC =gCDB =90*(vì EC vuông gAB,BD vuông gAC)
gEBC = gDCB(cmt)
=>tg BEC = tg CDB(ch-gn)
=>BD=EC
b)Theo phần a,ta có:tg BEC = tg CDB(ch-gn)
=>gDBC=gECB(2 góc tương ứng)
=>tg BIC cân tại I
=>BI=CI
mà EI+IC=EC và DI+BI=BD(vì I là gđ của BD và EC) và BD=EC(theo phần a)
=>EI = DI
c)Xét tg ABC ,có:
AB=AC(gt)
BI=CI(cmt)
BH=CH(vì H là trung điểm của BC)
=>Ba điểm A, I, H thẳng hàng

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
Suy ra: BD=CE
b: Xét ΔAED có AE=AD
nên ΔAED cân tại A
c: Xét ΔEBI vuông tại E và ΔDCI vuông tại D có
EB=DC
\(\widehat{EBI}=\widehat{DCI}\)
Do đó; ΔEBI=ΔDCI
Suy ra: IB=IC
Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc BAC

cách giải đây
\(\Delta ABC\)có AB = AC suy ra tam giác ABC tà tam giác cân
xét \(\Delta EBC\)và\(\Delta DCB\)
góc B = góc C ( tam giác cân )
BC là cạnh huyền chung
do đó tam giác EBC = tam giác DCB ( cạnh huyền - góc nhọn )
suy ra BD = CE ( 2 cạnh tương ứng )
b)
xét \(\Delta AHB\)và \(\Delta AHC\)có \(\hept{\begin{cases}AB=AC\left(gt\right)\\\widehat{B}=\widehat{C}\left(gt\right)\\BH=HC\left(gt\right)\end{cases}}\)
do đó \(\Delta AHB=\Delta AHC\left(c.g.c\right)\\ \Rightarrow\widehat{BAH}=\widehat{CAH}\)( 2 góc tương ứng)
xét tam giác vuông AIE và tam giác vuông AID có
AI là cạnh huyền chung
góc BAH = góc CAH ( cmt)
do đó tam giác AIE = tam giác AID ( cạnh huyền - góc nhọn )
suy ra EI = ID ( 2 cạnh tương ứng )
c) góc BAH = góc CAH mà tia AH nằm giữa tia AB và AC nên AH là phân giác góc BAC (1)
tam giác AIE = tam giác AID suy ra góc EAI = góc DAI ( 2 góc tương ứng )
mà tia AI nằm giữa 2 tia AE và AD suy ra AI là phân giác góc EAD hay góc BAC (2)
từ (1) và (2) suy ra ba điểm A;I:H thẳng hàng

chị làm đây ko bt đúng hay sai đâu nha
xét tam giác ABC có BD vuông góc với AC
CE vuông góc với AB
hai đường thẳng này cát nhau tại I
suy ra I là trực tâm của tam giác ABC
suy ra AI vuông góc với BC(1)
Mặt khác, M là trung điểm của BC=> AM là đường trung tuyến của tam giác ABC
mà trong 1 tam giác cân đường trung tuyến đồng thời là đường cao
<=> AM cũng là đường cao của tam giác ABC
=> AM vuông góc với BC(2)
từ (1)(2) ta có A,I,M thẳng hàng

3b)
Ta có tg BNK vuông tại K ->BN>BK
Ta có IK=MN(tính chất đoạn chắn)
Ta có : BC+MN=BK+KC+MN=BK+BI+IK=2BK
Vì BK<BN->2BK<2BN->BN>BK/2->BN>BC+MN/2

Xét tam giácBCE= tam giác CBD (cạnh huyền -mgóc nhọn)
góc ABC = góc ACB ( cân tại A)
BC chung
==> BD=CE
b) Tam giác BCE=tam giác CBD chứng minh ở câu a nên
góc BCE = góc DBC
--> IBC cân tại I


Xét tam giác vuông AEC và tam giác vuông ADB,có:
Góc A: chung
AB=AC ( ABC cân )
Vậy tam giác vuông AEC và tam giác vuông ADB ( ch.gn )
=> BD=CE ( 2 cạnh tương ứng )
b. bạn xem lại đề nhé
IH vuông góc vs BC I chỗ nào