Mọi người giúp với ạ.
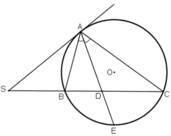
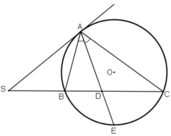
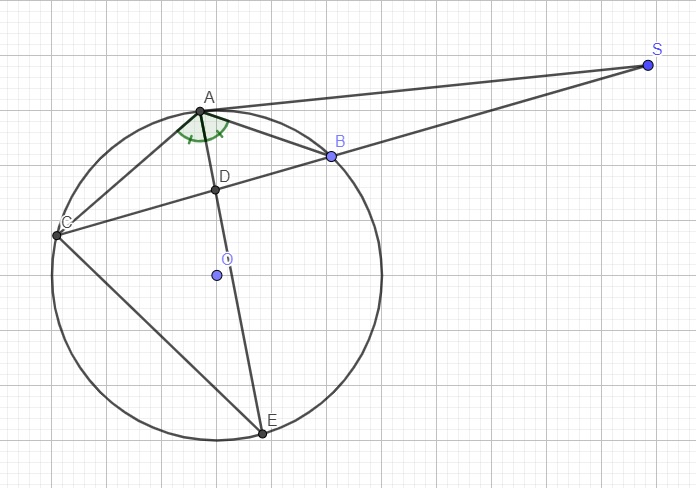
Cho một đường tròn tâm O và một điểm S nằm ngoài đường tròn. Vẽ tiếp tuyến SA và cát tuyến SBC ( B nằm giữa ). Phân giác của góc BAC cắt BC tại D. Chứng minh :
a, SA2= SB.SC
b, SA=SD
c, Trong tất cả các cát tuyến từ S thì cát tuyến qua tâm O là dài nhất.
d. Cho SA = 20, SC = 50. Tính R (O).
Ai biết thì giải dùm với. Cảm ơn nhiều.

 là góc có đỉnh nằm bên trong đường tròn
là góc có đỉnh nằm bên trong đường tròn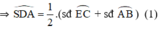
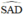 là góc tạo bởi tiếp tuyến AS và dây AE
là góc tạo bởi tiếp tuyến AS và dây AE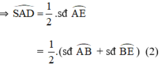
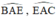 lần lượt là các góc nội tiếp chắn các cung
lần lượt là các góc nội tiếp chắn các cung 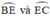
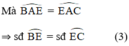
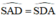
 là góc có đỉnh nằm bên trong đường tròn
là góc có đỉnh nằm bên trong đường tròn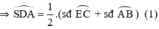
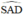 là góc tạo bởi tiếp tuyến AS và dây AE
là góc tạo bởi tiếp tuyến AS và dây AE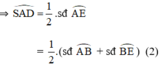
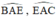 lần lượt là các góc nội tiếp chắn các cung
lần lượt là các góc nội tiếp chắn các cung 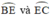
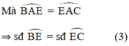
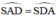

a) Ta có : Góc SAB = 1/2 sđ cung AB ( Góc tạo bởi tiếp tuyến và dây cung)
Góc SCA = 1/2 sđ cung AB (Góc nội tiếp)
=> Góc SAB = Góc SCA
Xét hai tam giác : \(\Delta SAB\)và \(\Delta SCA\)có : Góc ASC chung , Góc SAB = góc SCA
=> \(\Delta SAB~\Delta SCA\left(g.g\right)\)\(\Rightarrow\frac{SA}{SC}=\frac{SB}{SA}\Rightarrow SA^2=SB.SC\)
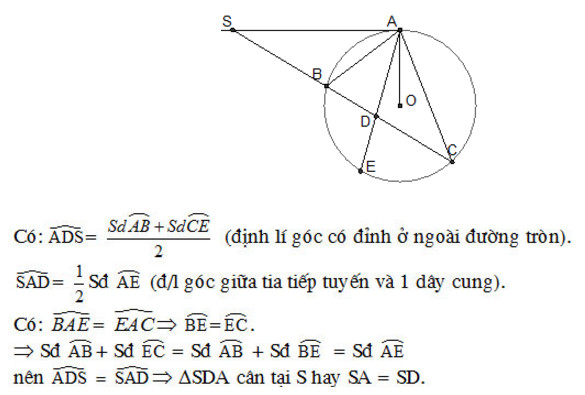
b) Ta có SDA là góc ngoài của tam giác ACD \(\Rightarrow SDA=DAC+DCA=DAC+\frac{1}{2}sdAB\)
Mặt khác, ta có ; \(SAD=BAD+\frac{1}{2}sdAB=DAC+\frac{1}{2}sdAB\)( Vì AD là tia phân giác)
Do đó góc SDA = góc SAD => Tam giác SAD cân tại S => SA = SD