Chứng minh bất đẳng thức : (X+a).(x+b)=x^2+(a+b)x+ab
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x+a\right)\left(x+b\right)\)
=>\(x^2+bx+ax+ab\)
=>\(x^2+\left(a+b\right)x+ab\)(ĐPCM)
Nhớ H cho mik nhé, các bạn.

a) Xét hàm số f(x) = tanx − sinx trên nửa khoảng [0; π/2);

x ∈ [0;1/2)
Dấu “=” xảy ra khi x = 0.
Suy ra f(x) đồng biến trên nửa khoảng [0; π/2)
Mặt khác, ta có f(0) = 0, nên f(x) = tanx – sinx > 0 hay tanx > sinx với mọi x ∈ [0; 1/2)
b) Xét hàm số h(x) trên [0; + ∞ )
![]()
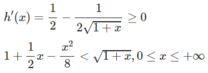
Dấu “=” xẩy ra chỉ tại x = 0 nên h(x) đồng biến trên nửa khoảng [0; + ∞ ).
Vì h(x) = 0 nên
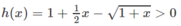
Hay
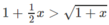
Xét hàm số trên f(x) trên [0; + ∞ );
![]()
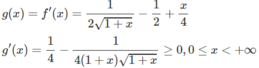
Vì g(0) = 0 và g(x) đồng biến trên nửa khoảng [0; + ∞ ) nên g(x) ≥ 0, tức là f′(x) ≥ 0 trên khoảng đó và vì dấu “=” xảy ra chỉ tại x = 0 nên f(x) đồng biến trên nửa khoảng .
Mặt khác, ta có f(0) = 0 nên
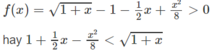
Với mọi 0 < x < + ∞ .

a)Có \(a^2+1\ge2a\) với mọi a; \(b^2+1\ge2b\) với mọi b
Cộng vế với vế \(\Rightarrow a^2+b^2+2\ge2\left(a+b\right)\)
Dấu = xảy ra <=> a=b=1
b) Áp dụng BĐT bunhiacopxki có:
\(\left(x+y\right)^2\le\left(1+1\right)\left(x^2+y^2\right)\Leftrightarrow\left(x+y\right)^2\le2\)
\(\Leftrightarrow-\sqrt{2}\le x+y\le\sqrt{2}\)
\(\Rightarrow\left(x+y\right)_{max}=\sqrt{2}\Leftrightarrow\left\{{}\begin{matrix}x+y=\sqrt{2}\\x=y\end{matrix}\right.\)\(\Leftrightarrow x=y=\dfrac{\sqrt{2}}{2}\)
\(\left(x+y\right)_{min}=-\sqrt{2}\Leftrightarrow\left\{{}\begin{matrix}x+y=-\sqrt{2}\\x=y\end{matrix}\right.\)\(\Leftrightarrow x=y=-\dfrac{\sqrt{2}}{2}\)
c) \(S=\dfrac{1}{ab}+\dfrac{1}{a^2+b^2}=\dfrac{1}{a^2+b^2}+\dfrac{1}{2ab}+\dfrac{1}{2ab}\)
Với x,y>0, ta có: \(\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y}\) (1)
Thật vậy (1) \(\Leftrightarrow\dfrac{y+x}{xy}\ge\dfrac{4}{x+y}\Leftrightarrow\left(x+y\right)^2\ge4xy\)\(\Leftrightarrow\left(x-y\right)^2\ge0\) (lđ)
Áp dụng (1) vào S ta được:
\(S\ge\dfrac{4}{a^2+b^2+2ab}+\dfrac{1}{2ab}\)
Lại có: \(ab\le\dfrac{\left(a+b\right)^2}{4}\) \(\Leftrightarrow2ab\le\dfrac{\left(a+b\right)^2}{2}\Leftrightarrow2ab\le\dfrac{1}{2}\)\(\Rightarrow\dfrac{1}{2ab}\ge2\)
\(\Rightarrow S\ge\dfrac{4}{\left(a+b\right)^2}+2=6\)
\(\Rightarrow S_{min}=6\Leftrightarrow a=b=\dfrac{1}{2}\)

Lời giải:
$x^2+x+1=x^2+2.x.\frac{1}{2}+(\frac{1}{2})^2+\frac{3}{4}$
$=(x+\frac{1}{2})^2+\frac{3}{4}$
$\geq 0+\frac{3}{4}$
$> 0$
Ta có đpcm.

a) VT = ( a + b + a − b ) ( a + b − a + b ) 4 = 2 a . 2 b 4 = 4 = VP => đpcm.
b) VP = x 2 + 2 xy + y 2 + x 2 – 2 xy + y 2 = 2 ( x 2 + y 2 ) = VT => đpcm.


\(\dfrac{\left(a+b\right)^2-\left(a-b\right)^2}{4}=\dfrac{a^2+2ab+b^2-a^2+2ab-b^2}{4}=\dfrac{4ab}{4}=ab\left(đpcm\right)\)
\(\left(x+y\right)^2+\left(x-y\right)^2=x^2+2xy+y^2+x^2-2xy+y^2=2x^2+2y^2=2\left(x^2+y^2\right)\left(dpcm\right)\)

a. \(VT=\left(x+a\right)\left(x+b\right)=x^2+ã+bx+ab=x^2+\left(a+b\right)x+ab=VP\)
B. \(VT=\left(x+a\right)\left(x+b\right)\left(x+c\right)=\left[\left(x+a\right)\left(x+b\right)\right].\left(x+c\right)\)
\(=\left[\left(x^2+\left(a+b\right)x\right)+ab\right].\left(x+c\right)=x^3+x^2c+\left(a+b\right)x^2+c\left(a+b\right)x+abx+abc\)
\(=x^3+\left(a+b+c\right)x^2+\left(ab+bc+ca\right)x+abc=VP\)

Lời giải:
Ta có:
$x^4+y^4+(x+y)^4=(x^4+y^4+2x^2y^2)-2x^2y^2+[(x+y)^2]^2$
$=(x^2+y^2)^2-2x^2y^2+(x^2+2xy+y^2)^2$
$=(x^2+y^2)^2-2x^2y^2+(x^2+y^2)^2+(2xy)^2+4xy(x^2+y^2)$
$=2(x^2+y^2)^2+2x^2y^2+4xy(x^2+y^2)$
$=2[(x^2+y^2)^2+2xy(x^2+y^2)+(xy)^2]$
$=2(x^2+y^2+xy)^2$
Ta có đpcm.
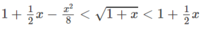
Cái này nhân ra rồi nhóm lại thôi mÀ
(x+a).(x+b)=x2+bx+ax+ab
=x2+(a+b)x+ab=VP (Đpcm)