1+2+22+23+24+...+2n
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1+2+2^2+2^3+...+2^n=357680\)
\(\Leftrightarrow2\cdot\left(1+2+2^2+...+2^n\right)=2\cdot357680\)
\(\Leftrightarrow2+2^2+2^3+2^4+...+2^{n+1}=2\cdot357680\)
\(\Leftrightarrow\left(2+2^2+...+2^{n+1}\right)-\left(1+2+2^2+...+2^n\right)=2\cdot357680-357680\)
\(\Leftrightarrow\left(2-2\right)+\left(2^2-2^2\right)+...+\left(2^n-2^n\right)+\left(2^{n+1}-1\right)=357680\)
\(\Leftrightarrow2^{n+1}-1=357680\)
\(\Leftrightarrow2^{n+1}=357681\)
Xem lại đề
\(1+2+2^2+2^3+...+2^n=357680\)
\(\Rightarrow\dfrac{2^{n+1}-1}{2-1}=357680\)
\(\Rightarrow2^{n+1}=357680+1\)
\(\Rightarrow2^{n+1}=357681\Rightarrow n+1=\sqrt[]{357681}\Rightarrow n=\sqrt[]{357681}-1\)

Lúa nước mất 1 NST cặp số 12
Lúa nước mất 1 cặp NST số 2

Lời giải:
$C=1-2+2^2-2^3+2^4-....+2^{2022}$
$2C=2-2^2+2^3-2^4+2^5-...+2^{2023}$
$\Rightarrow C+2C=(1-2+2^2-2^3+2^4-....+2^{2022})+(2-2^2+2^3-2^4+2^5-...+2^{2023})$
$\Rightarrow 3C=2^{2023}-1$
$\Rightarrow C=\frac{2^{2023}-1}{3}$


Đặt A = \(1+2+2^2+2^3+2^4+....+2^{100}\)
2A = \(2\left(1+2+2^2+2^3+2^4+....+2^{100}\right)\)
= \(2+2^2+2^3+2^4+2^5+...+2^{101}\)
2A - A = \(\left(2+2^2+2^3+2^4+2^5+....+2^{101}\right)-\left(1+2^2+2^3+2^4+...+2^{100}\right)\)
= \(2^{101}-1\)

1−2−3+4+5−6−7+8+...+21−22−23+24+25
= (1 - 2 - 3 + 4) + (5 - 6 - 7 + 8) + ... + (21 - 22 - 23 + 24) + 25=(1−2−3+4)+(5−6−7+8)+...+(21−22−23+24)+25
= 0 + 0 + ... + 0 + 25=0+0+...+0+25
= 25

\(2A=2-2^2+2^3-...-2^{30}+2^{31}\\ \Leftrightarrow2A+A=2-2^2+2^3-...-2^{30}+2^{31}+1-2+2^2-...-2^{29}+2^{30}\\ \Leftrightarrow3A=2^{31}+1\\ \Leftrightarrow A=\dfrac{2^{31}+1}{2}\)
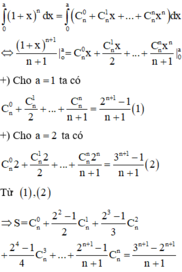

Đặt A là biểu thức trên ta có:
2A = 2 + 22 + 23 + ..... + 2(n+1)
2A - A = 2(n+1) - 1
A = 2(n+1) - 1
Ta có: \(A=1+2+2^2+2^3+2^4+...+2^n\)
Ta lại có: \(2A=2+2^2+2^3+2^4+2^5+...+2^{n+1}\)
\(2A-A=A=2^{n+1}-1\)
\(A=\frac{2^{n+1}-1}{2}\)