Làm giúp em câu 17 18 19:((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


16.
\(\lim\dfrac{u_n}{v_n}=+\infty\)
17.
\(SA\perp\left(ABC\right)\Rightarrow SA\perp AB\Rightarrow\Delta SAB\) vuông tại A (B đúng)
\(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\) (C đúng)
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\) (D đúng)
18.
Tập hợp điểm cách đều 2 điểm AB cho trước là mặt phẳng trung trực của AB
19.
\(\lim\limits_{x\rightarrow1}\dfrac{x-1}{2x-2}=\lim\limits_{x\rightarrow1}\dfrac{x-1}{2\left(x-1\right)}=\dfrac{1}{2}\)
vào thế kỉ 16, 17, 18, 19, 20 có mấy loài thú tuyệt chủng
Giúp em với cần gấp câu tl thật chính xác ạ


Bạn ơi, mik mới học lớp 8 thôi, bạn giải dùng nhiều kí tự mik ko hiểu, bạn có cách khác ko, hiện tại mik chỉ mới học hằng đẳng thức thôi ạ. Nhưng vẫn cảm ơn bạn rất nhiều bạn nha.

17.
Gọi số vi khuẩn ban đầu là x
Sau 5 phút số vi khuẩn là: \(x.2^5=64000\Rightarrow x=2000\)
Sau k phút:
\(2000.2^k=2048000\Rightarrow2^k=1024=2^{10}\)
\(\Rightarrow k=10\)
18.
\(S_{2019}=\left(\dfrac{1}{2}\right)^1+1+\left(\dfrac{1}{2}\right)^2+1+...+\left(\dfrac{1}{2}\right)^{2019}+1\)
\(=\left(\dfrac{1}{2}\right)^1+\left(\dfrac{1}{2}\right)^2+...+\left(\dfrac{1}{2}\right)^{2019}+2019\)
Xét \(S=\left(\dfrac{1}{2}\right)^1+\left(\dfrac{1}{2}\right)^2+...+\left(\dfrac{1}{2}\right)^{2019}\) là tổng cấp số nhân với \(\left\{{}\begin{matrix}u_1=\dfrac{1}{2}\\q=\dfrac{1}{2}\\n=2019\end{matrix}\right.\)
\(\Rightarrow S=\dfrac{1}{2}.\dfrac{\left(\dfrac{1}{2}\right)^{2019}-1}{\dfrac{1}{2}-1}=1-\dfrac{1}{2^{2019}}\)
\(\Rightarrow S_{2020}=2019+S=2020-\dfrac{1}{2^{2019}}\)
19. C là khẳng định sai, ví dụ: \(u_n=2\) ; \(v_n=-\dfrac{1}{n}\)

17)
a)
\(CH_3-CH_3\underrightarrow{t^o,xt}CH_2=CH_2+H_2\)
\(CH_2=CH_2+Br_2\rightarrow CH_2Br-CH_2Br\)
\(CH_2Br-CH_2Br+2KOH\underrightarrow{ancol,t^o}CH\equiv CH+2KBr+2H_2O\)
\(CH\equiv CH+H_2O\underrightarrow{HgSO_4,H_2SO_4}CH_3CHO\)
b)
\(CaC_2+2H_2O\rightarrow Ca\left(OH\right)_2+CH\equiv CH\)
\(2CH\equiv CH\underrightarrow{đime.hóa}CH\equiv C-CH=CH_2\)
\(CH\equiv C-CH=CH_2+H_2\underrightarrow{t^o,Pd/PbCO_3}CH_2=CH-CH=CH_2\)
\(nCH_2=CH-CH=CH_2\underrightarrow{t^o,p,Na}\left(-CH_2-CH=CH-CH_2-\right)_n\)
c)
\(Al_4C_3+12H_2O\rightarrow4Al\left(OH\right)_3+3CH_4\)
\(2CH_4\underrightarrow{1500^oC,làm.lạnh.nhanh}CH\equiv CH+3H_2\)
\(CH\equiv CH+H_2\underrightarrow{t^o,Pd/PbCO_3}CH_2=CH_2\)
\(CH_2=CH_2+H_2O\underrightarrow{t^o,H_2SO_4}CH_3-CH_2OH\)
\(CH_3-CH_2OH+3O_2\underrightarrow{t^o}2CO_2+3H_2O\)
d)
\(CH_3-CH_2OH\underrightarrow{170^oC,H_2SO_4}CH_2=CH_2+H_2O\)
\(CH_2=CH_2+HCl\rightarrow CH_3-CH_2Cl\)
\(CH_3-CH_2Cl+KOH\underrightarrow{t^o,ancol}CH_2=CH_2+KCl+H_2O\)
\(nCH_2=CH_2\underrightarrow{t^o,p,xt}\left(-CH_2-CH_2-\right)_n\)
\(\)
18)
- Trích một ít các chất làm mẫu thử
a)
- Cho các khí tác dụng với dd AgNO3/NH3
+ Không hiện tượng: C2H6, C2H4 (1)
+ Kết tủa vàng: C2H2
\(C_2H_2+2AgNO_3+2NH_3\rightarrow C_2Ag_2+2NH_4NO_3\)
- Dẫn các khí còn lại ở (1) tác dụng với dd Br2 dư:
+ dd nhạt màu dần: C2H4
\(C_2H_4+Br_2\rightarrow C_2H_4Br_2\)
+ Không hiện tượng: C4H10
b)
- Dẫn các khí qua dd AgNO3/NH3:
+ Không hiện tượng: C4H10, \(CH_3-C\equiv C-CH_3\) (1)
+ Kết tủa vàng: \(CH\equiv C-CH_2-CH_3\)
\(CH\equiv C-CH_2-CH_3+AgNO_3+NH_3\rightarrow CAg\equiv C-CH_2-CH_3\downarrow+NH_4NO_3\)
- Dẫn các khí còn lại ở (1) tác dụng với dd Br2 dư
+ dd nhạt màu dần: \(CH_3-C\equiv C-CH_3\)
\(CH_3-C\equiv C-CH_3+2Br_2\rightarrow CH_3-CBr_2-CBr_2-CH_3\)
+ Không hiện tượng: C2H6
c)
- Dẫn các khí qua dd AgNO3/NH3:
+ Kết tủa vàng: \(CH\equiv C-CH_3\)
\(CH\equiv C-CH_3+AgNO_3+NH_3\rightarrow CAg\equiv C-CH_3\downarrow+NH_4NO_3\)
+ Không hiện tượng: C2H6, \(CH_2=CH-CH=CH_2\) (1)
- Dẫn các khí còn lại ở (1) tác dụng với dd Br2 dư
+ dd nhạt màu dần: \(CH_2=CH-CH=CH_2\)
\(CH_2=CH-CH=CH_2+2Br_2\rightarrow CH_2Br-CHBr-CHBr-CH_2Br\)
+ Không hiện tượng: C2H6


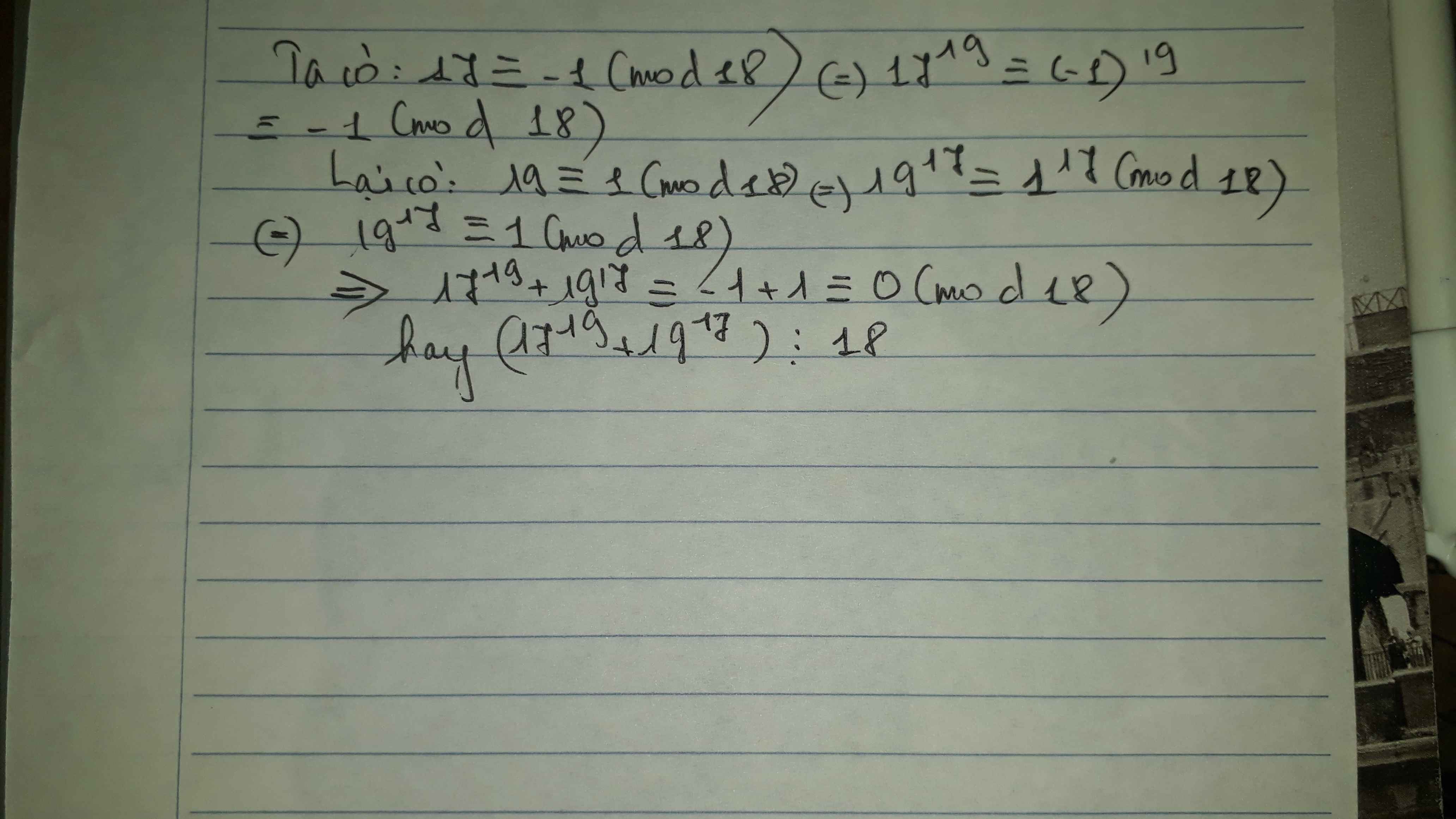








Câu 17: A
Câu 18: B
Câu 19: A
\(c17;f\left(x\right)=x^2-\left(m+2\right)x+4m+1\)
\(\Leftrightarrow\Delta>0\Leftrightarrow\left(m+2\right)^2-4\left(4m+1\right)=m^2-12m>0\Leftrightarrow\left[{}\begin{matrix}m< 0\\m>12\end{matrix}\right.\)
\(c18:\)\(x^2-2\left(m+1\right)x+m^2+3< 0\)
\(\Leftrightarrow\Delta'\le0\Leftrightarrow\left(m+1\right)^2-m^2-3\le0\Leftrightarrow m\le1\)
\(c19:\Leftrightarrow\Delta'\ge0\Leftrightarrow m^2-1\ge0\Leftrightarrow m^2\ge1\Leftrightarrow\left|m\right|\ge1\)