giải phuwng trình
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BG
cho a =2(1^2+2^2+3^2+4^2+....+2012^2+2013^2)hỏi a có phải là bình phuwng của một số nguyên hay không
0
12 tháng 11 2017
\(2NaOH+CuCl_2\rightarrow2NaCl+Cu\left(OH\right)_2\)
\(CuCl_2+Fe\rightarrow FeCl_2+Cu\)
\(BaCl_2+Na_2SO_4\rightarrow BaSO_4+2NaCl\)
\(BaCl_2+H_2SO_4\rightarrow BaSO_4+2HCl\)
\(Cu\left(OH\right)_2+H_2SO_4\rightarrow CuSO_4+2H_2O\)
NM
Nguyễn Minh Quang
Giáo viên
5 tháng 3 2022
ta có :
\(\left|x+1\right|+\left|x-1\right|=1+\left|\left(x-1\right)\left(x+1\right)\right|\)
\(\Leftrightarrow\left|x-1\right|\left|x+1\right|-\left|x-1\right|-\left|x+1\right|+1=0\)
\(\Leftrightarrow\left(\left|x-1\right|-1\right)\left(\left|x+1\right|-1\right)=0\Leftrightarrow\orbr{\begin{cases}\left|x-1\right|=1\\\left|x+1\right|=1\end{cases}}\)
\(\Leftrightarrow x\in\left\{-2,0,2\right\}\)
23 tháng 7 2021
Bài 1:
a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)
\(\Leftrightarrow6-8x-10+2x-5=0\)
\(\Leftrightarrow-6x+11=0\)
\(\Leftrightarrow-6x=-11\)
hay \(x=\dfrac{11}{6}\)
b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)
\(\Leftrightarrow6-12x-11+3x-1=0\)
\(\Leftrightarrow-9x-6=0\)
\(\Leftrightarrow-9x=6\)
hay \(x=-\dfrac{2}{3}\)
CM
2 tháng 11 2017
a) Cách giải các phương trình lượng giác cơ bản:
+ Phương trình sin x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho sin α = a.
Khi đó phương trình trở thành sin x = sin α
⇒ Phương trình có nghiệm: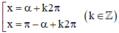 
+ Phương trình cos x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho cos α = a.
Khi đó phương trình trở thành cos x = cos α.
⇒ Phương trình có nghiệm: x = ±α + k2π (k ∈ Z).
+ Phương trình tan x = a.
Tìm một cung α sao cho tan α = a.
Khi đó phương trình trở thành tan x = tan α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
+ Phương trình cot x = a
Tìm một cung α sao cho cot α = a.
Khi đó phương trình trở thành cot x = cot α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
b) Cách giải phương trình a.sin x + b.cos x = c.
+ Nếu a = 0 hoặc b = 0 ⇒ Phương trình lượng giác cơ bản .
+ a ≠ 0 và b ≠ 0. Chia cả hai vế của phương trình cho 
ta được:
Ta giải phương trình trên như phương trình lượng giác cơ bản.
ML
13 tháng 3 2021
Bài 1:
Thuật toán:
B1: Nhập a,b,c
B2: Tính \(\Delta\) = b2-4ac;
B3: Kiểm tra nếu \(\Delta\) >0 phương trình có 2 nghiệm phân biệt
\(x_1=\dfrac{-b+\sqrt{\Delta}\text{ }}{2a}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}\)
B4: Kiểm tra nếu \(\Delta\)<0 thì phương trình vô nghiệm
B5: Kiểm tra nếu \(\Delta\)=0 phương trình có 2 nghiệm kép \(x_1=x_2=-\dfrac{b}{2a}\)
Viết chương trình:
Program HOC24;
var a,b,c: integer;
x1,x2: real;
denta: longint;
begin
write('Nhap a; b; c: '); readln(a,b,c);
denta:=b*b-4*a*c;
if denta>0 then
begin
write('x1= ',(-b+sqrt(denta))/(2*a):1:2);
write('x2= ',(-b-sqrt(denta))/(2*a):1:2);
end;
if denta<0 then write('Phuong trinh vo nghiem');
if denta=0 then write('x= ',-b/2*a:1:2);
readln
end.
ML
13 tháng 3 2021
Bài 2:
Thuật toán:
B1: Nhập a,b
B2: Kiểm tra nếu a=0 và b=0 thì phương trình có vô số nghiệm
B3: Kiểm tra nếu a=0 thì phương trình vô nghiệm
B4: Kiểm tra nếu a khác 0 thì có nghiệm x=-b/a;
Viết chương trình:
Program HOC24;
var a,b: integer;
x: real;
begin
write('Nhap a; b: '); readln(a,b);
if a=0 and b=0 then write('Phuong trinh co vo so nghiem');
if a=0 then write('Phuong trinh vo nghiem');
if a<>0 then write('x=',-b/a:1:2);
readln
end.
. Ta có:
CM
9 tháng 3 2017
a) Sai lầm là coi -2 là hạng từ và chuyển vế hạng tử này trong khi -2 là một nhân tử.
Lời giải đúng:
-2x > 23
⇔ x < 23 : (-2) (chia cho số âm nên đổi chiều)
⇔ x < -11,5
Vậy nghiệm của bất phương trình là x < -11,5
b) Sai lầm là nhân hai vế của bất phương trình với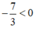 
mà không đổi chiều bất phương trình.
Lời giải đúng:
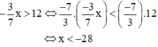
Vậy nghiệm của bất phương trình là x < -28
DK
28 tháng 2 2017
Chọn đáp án C
Các phát biểu II, III, IV đúng. Đáp án C
I – Sai. Vì hô hấp sáng không tạo ra ATP
`Answer:`
`a)7x+21=0`
`<=>7x=-21`
`<=>x=-21:7`
`<=>x=-3`
`b)3x+1=7x-11`
`<=>3x-7x=-11-1`
`<=>-4x=-12`
`<=>x=3`
`c)4/3x-5/6=1/2`
`<=>4/3x=1/2+5/6`
`<=>4/3x=4/3`
`<=>x=1`
`d)\frac{x-3}{5}=1-\frac{1-2x}{3}`
`<=>3(x-3)=15-5(1-2x)`
`<=>3(x-3)-15+5(1-2x)=0`
`<=>3x-9-15+5-10x=0`
`<=>-7x-19=0`
`<=>-7=19`
`<=>x=\frac{-19}{7}`
`e)\frac{2x}{3}+\frac{2x-1}{6}=4-x/3`
`<=>2.2x+2x-1=4.6-2x`
`<=>4x+2x-1=24-2x`
`<=>6x+2x=24+1`
`<=>8x=25`
`<=>x=\frac{25}{8}`
`f)(4x-10)(24+5x)=0`
`<=>2(2x-5)(24+5x)=0`
`<=>2x-5=0` hoặc `24+5x=0`
`<=>x=5/2` hoặc `x=\frac{-24}{5}`
`g)x^2+1=x(x-1)`
`<=>x^2+1=x^2-x`
`<=>x^2-x^2=-x-1`
`<=>-x-1=0`
`<=>-x=1`
`<=>x=-1`
`h)
`i)\frac{2x^2-3x-2}{x^2-4}=2(ĐKXĐ:x\ne+-2)`
`<=>\frac{2x^2-4x+x-2}{(x-2)(x+2)}=2`
`<=>\frac{2x+1}{x+2}=2`
`<=>2x+1=2x+4`
`<=>1=4` (Vô lý)
Vậy phương trình vô nghiệm.
`i)\frac{x-1}{x+1}+3=\frac{2x+3}{x+1}(ĐK:x\ne-1)`
`<=>3=\frac{2x+3}{x+1}-\frac{x-1}{x+1}`
`<=>\frac{2x+3-x+1}{x+1}=3`
`<=>\frac{x+4}{x+1}=3`
`<=>3(x+1)=x+4`
`<=>3x+3=x+4`
`<=>2x=1`
`<=>x=1/2`