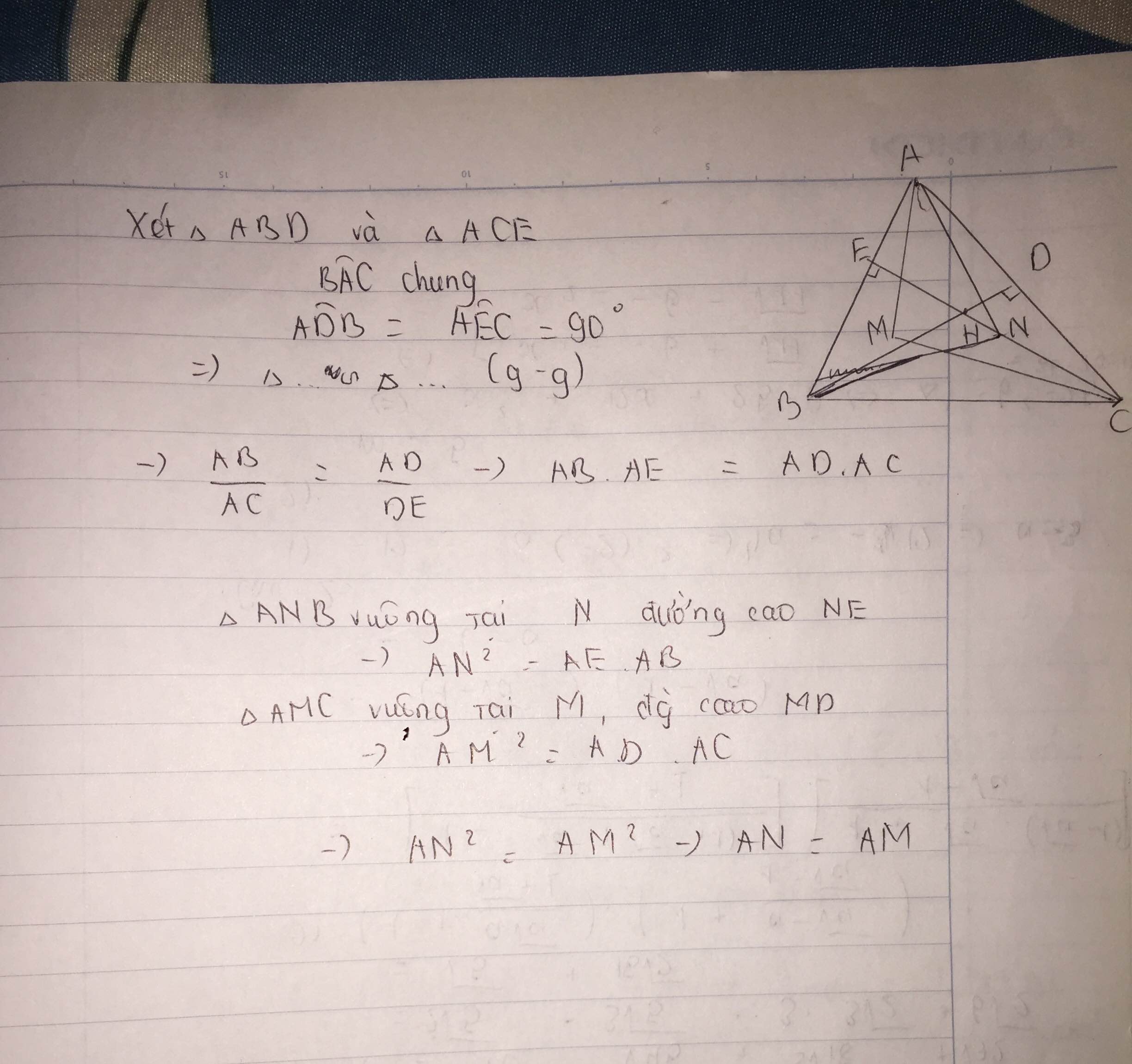Cho tam giác ABC nhọn, đường cao BD và CE cắt nhau tại H. Chứng minh: P, H. BD + CH. CE = BC2.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gợi ý: Gọi  , chứng minh được AK ^ BC.
, chứng minh được AK ^ BC.
Áp dụng cách làm tương tự 4A suy ra ĐPCM

a) Chứng minh tam giác AED đông dang tam giác ACB
b) Kẻ HI vuông góc BC
Có BHxBD+CHxCE=BC^2 bằng xét 2 cặp tam giác đông dạng.

Cho tam giác nhọn ABC có hai đường cao BD và CE căt nhau tại H .
Chứng minh rằng : BC^2=BH.BD+CH.CE
Bài này em có thể giải như sau
1)1) Ta có:
△CDH∼△ACE (g.g)△CDH∼△ACE (g.g)
⇒CHAE=CDAC⇒CH.AC=AE.CD=AB.AE⇒CHAE=CDAC⇒CH.AC=AE.CD=AB.AE
△ADH∼△ACF (g.g)△ADH∼△ACF (g.g)
⇒ADAC=AHAF⇒AH.AC=AD.AF⇒ADAC=AHAF⇒AH.AC=AD.AF
Do đó: AC2=AH.AC+CH.AC=AB.AE+AD.AFAC2=AH.AC+CH.AC=AB.AE+AD.AF
2)2) Dựng HFHF vuông góc BC.BC. Ta có:
△BFH∼△BDC△BFH∼△BDC
⇒BFBD=BHBC⇒BF.BC=BD.BH⇒BFBD=BHBC⇒BF.BC=BD.BH
△CFH∼△CEB△CFH∼△CEB
⇒CF/CE=CHCB⇒CF.BC=CE.CH⇒CFCE=CHCB⇒CF.BC=CE.CH
Do đó: BC^2=BF.BC+CF.BC=BD.BH=CE.CH
các dấu kí tự bạn tự thêm nhé

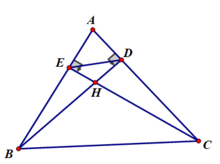
b) Xét tứ giác BDEC có:
∠(BEC) = ∠(BDC) = 90 0
Mà 2 góc này cùng nhìn cạnh BC
⇒ Tứ giác BDEC là tứ giác nội tiếp

Xin lỗi bạn nhưng máy mình bị lỗi không vẽ hình được.
c) Tứ giác BEDC là tứ giác nội tiếp (câu a) \(\Rightarrow\widehat{BDE}=\widehat{BCE}\) hay \(\Rightarrow\widehat{BDE}=\widehat{BCQ}\) (1)
Xét (O) có \(\widehat{BCQ}\) và \(\widehat{BPQ}\) là các góc nội tiếp chắn \(\stackrel\frown{BQ}\) \(\Rightarrow\widehat{BCQ}=\widehat{BPQ}\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{BDE}=\widehat{BPQ}\left(=\widehat{BCQ}\right)\)
\(\Rightarrow DE//PQ\) (2 góc đồng vị bằng nhau)
d) Kẻ tia tiếp tuyến Ax của (O) (ở đây mình lấy về phía B chứ còn bạn lấy tia tiếp tuyến này vế phía B hay phía C tùy)
Dễ thấy \(\widehat{BAx}\) và \(\widehat{ACB}\) lần lượt là góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn \(\stackrel\frown{AB}\) \(\Rightarrow\widehat{BAx}=\widehat{ACB}\)
Tứ giác BEDC nội tiếp \(\Rightarrow\widehat{AED}=\widehat{ACB}\) (góc ngoài = góc trong đối)
\(\Rightarrow\widehat{BAx}=\widehat{AED}\left(=\widehat{ACB}\right)\) \(\Rightarrow Ax//DE\) ( 2 góc so le trong bằng nhau)
Vì \(DE//PQ\left(cmt\right)\) \(\Rightarrow Ax//PQ\)\(\left(//DE\right)\)
Mà \(Ax\perp OA\) tại A (do Ax là tiếp tuyến tại A của (O)) \(\Rightarrow OA\perp PQ\) (3)
Xét (O) có OA là 1 phần đường kính và \(OA\perp PQ\left(cmt\right)\)
\(\Rightarrow\) OA đi qua trung điểm của PQ (4)
Từ (3) và (4) \(\Rightarrow\) OA là trung trực của đoạn PQ