Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a tâm O, SA⊥(ABCD), \(SA=a\sqrt{6}\) . Tính góc giữa đường thẳng SC và mặt phẳng (ABCD)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow\widehat{BSC}\) là góc giữa SC và (SAB)
\(tan\widehat{BSC}=\dfrac{BC}{SB}=\dfrac{\sqrt{10}}{5}\Rightarrow SB=\dfrac{a\sqrt{10}}{2}\)
\(\Rightarrow SA=\sqrt{SB^2-AB^2}=\dfrac{a\sqrt{6}}{2}\)
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SOA}\) là góc giữa SO và (ABCD)
\(AO=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\)
\(tan\widehat{SOA}=\dfrac{SA}{AO}=\sqrt{3}\Rightarrow\widehat{SOA}=60^0\)

Đáp án A.
Gọi H là hình chiếu của C trên SO và góc S O C ^ tù nên H nằm ngoài đoạn SO => CH ⊥ (SBD)
=> Góc tạo bởi SC và (SBD) là C S O ^
Lại có ![]()
![]()
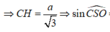
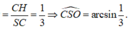

Đáp án A
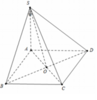
Ta có C B ⊥ A B C B ⊥ S A ⇒ C B ⊥ ( S A B )
Do đó S C ; S A B ^ = C S B ^ = α
⇒ S B = a tan α = 5 a 10 ⇒ S A = S B 2 - A B 2 = a 6 2
Ta có S O ; A B C D ^ = S O A ^ trong đó t a n S C A ^ = S A O A = a 6 2 a 2 2 = 3 .


Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
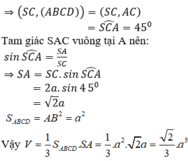

CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
=>(SC;(SAD))=(SC;SD)=góc DSC
SD=căn SA^2+AD^2=a*căn 7
DC=a
SC=căn SA^2+AC^2=3a
\(cosDSC=\dfrac{SD^2+SC^2-DC^2}{2\cdot SD\cdot SC}=\dfrac{9a^2+7a^2-a^2}{2\cdot3a\cdot a\sqrt{7}}=\dfrac{5\sqrt{7}}{14}\)
=>góc DSC=19 độ

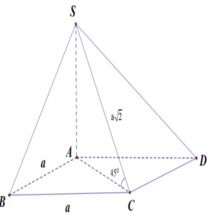
Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
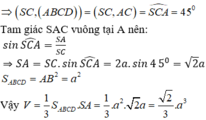

Đáp án C
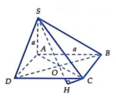
Gọi H là hình chiếu của C trên SO(O = AC ∩ BD), vì góc SOC tù nên H nằm ngoài SO
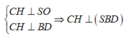
=> Góc tạo bởi SC và (SBD) là C S O ^
Ta có ![]()
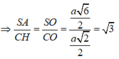
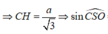
![]()
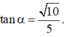
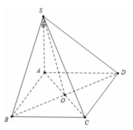


\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\dfrac{a\sqrt{6}}{a\sqrt{2}}=\sqrt{3}\)
\(\Rightarrow\widehat{SCA}=60^0\)