cho tam giác ABC [ A = 90 độ ] , hạ AH vuông hóc với BC [ H thuộc BC ]. Trên tia đối tia HA lấy điểm D sao cho HA = HD a, chứng minh AB = DB b, chứng minh CAB = CDB . Có vẽ hình và làm cả câu a,b nha mọi người
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
11 tháng 11 2023
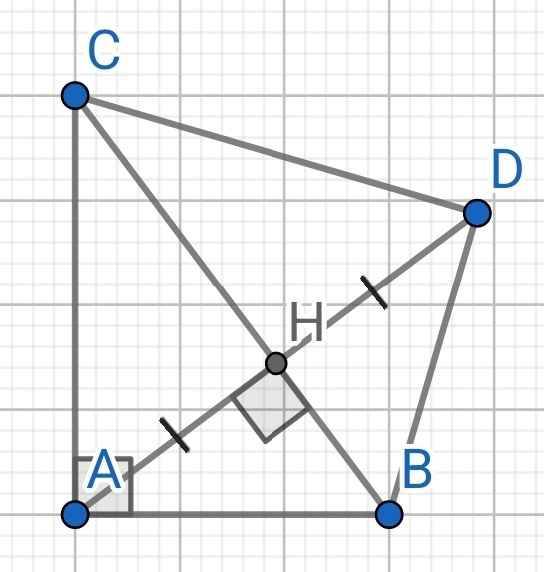a) Xét hai tam giác vuông: ∆ABH và ∆DBH có:
AH = DH (gt)
BH là cạnh chung
⇒ ∆ABH = ∆DBH (hai cạnh góc vuông)
b) Sửa đề: Chứng minh ∠BDC = 90⁰
Do ∆ABH = ∆DBH (cmt)
⇒ ∠ABH = ∠DBH (hai góc tương ứng)
AB = BD (hai cạnh tương ứng)
Do ∠ABH = ∠DBH (cmt)
⇒ ∠ABC = ∠DBC
Xét ∆ABC và ∆DBC có:
AB = BD (cmt)
∠ABC = ∠DBC (cmt)
BC là cạnh chung
⇒ ∆ABC = ∆DBC (c-g-c)
⇒ ∠BAC = ∠BDC = 90⁰
Vậy ∠BDC = 90⁰
9 tháng 7 2023
a: góc B=90-30=60 độ
góc B>góc C
=>AC>AB
góc CAH=90-30=60 độ>góc C
=>CH>AH
b: Xét ΔAHC vuông tại H và ΔDHC vuông tại H có
CH chung
HA=HD
=>ΔCAH=ΔCDH
c: Xét ΔACB và ΔDCB có
CA=CD
góc ACB=góc DCB
CB chung
=>ΔACB=ΔDCB
=>góc CDB=góc CAB=90 độ
20 tháng 12 2020
a) Xét ΔBHA vuông tại H và ΔBHD vuông tại H có
BH chung
AH=DH(gt)
Do đó: ΔBHA=ΔBHD(hai cạnh góc vuông)
b) Xét ΔHBA vuông tại H và ΔHKD vuông tại H có
HB=HK(gt)
HA=HD(gt)
Do đó: ΔHBA=ΔHKD(hai cạnh góc vuông)
⇒\(\widehat{HBA}=\widehat{HKD}\)(hai góc tương ứng)
mà \(\widehat{HBA}\) và \(\widehat{HKD}\) là hai góc ở vị trí so le trong
nên AB//DK(Dấu hiệu nhận biết hai đường thắng song song)
c) Ta có: AB//DK(cmt)
AB⊥AC(ΔABC vuông tại A)
Do đó: DK⊥AC
Xét ΔDAK có
KH là đường cao ứng với cạnh AD(KH⊥AD)
AC là đường cao ứng với cạnh DK(AC⊥DK)
KH\(\cap\)AC={C}
Do đó: C là trực tâm của ΔDAK(Tính chất ba đường cao của tam giác)
⇒DC⊥AK(đpcm)
14 tháng 12 2022
1) Áp dụng t/c tổng 3 góc trog 1 tg ta có:
(các góc trog )
Khi đó:
(quan hệ góc và cạnh đối diện)
(quan hệ đường xiên hình chiếu)
2) Có vấn đề.
3) Xét vuông tại H và vuông tại H có:
chung
4) Vì
nên
C/m tương tự câu 3):
Áp dụng tc tổng 3 góc trog 1 tg ta có:
18 tháng 4 2021
a) Xét tam giác ABC cân tại A: AH là đường cao (AH vuông góc với BC)
=> AH là đường trung tuyến (TC tam giác cân)
=> H à TĐ của BC
=> BH = HC
Xét tam giác AHB và tam giác AHC:
BH = HC (cmt)
^AHB = ^AHC (90o)
AH chung
=> tam giác AHB = tam giác AHC (ch - cgv)
b) Ta có: HA = HD (gt) => H là TĐ của AD
Xét tam giác ACD có:
CH là đường cao (CH vuông góc AD)
CH là trung tuyến (H là TĐ của AD)
=> tam giác ACD cân tại C
c) Xét tam giác ACD cân tại A có:
AD > AC + CD (Bất đẳng thức trong tam giác)
=> \(\dfrac{1}{2}AD=\dfrac{1}{2}\left(AC+CD\right)\)
Mà \(HA=\dfrac{1}{2}AD\) (H là TĐ của AD)
=> \(HA>\dfrac{1}{2}\left(AC+CD\right)\) (ĐPCM)
18 tháng 4 2021
Bạn có thể giúp mik thêm 1 cái nx là vẽ hình đc ko bạn?
a: Xét ΔBAD có
BH là đường cao
BH là đường trung tuyến
Do đó: ΔBAD cân tại B
b: Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAD cân tại C
Xét ΔCAB và ΔCDB có
CA=CD
CB chung
AB=DB
Do đó: ΔCAB=ΔCDB
Suy ra: \(\widehat{CAB}=\widehat{CDB}\)