Cho tam giác ABC. Qua A vẽ đường thẳng a//BC. Qua B vẽ đường thẳng b//AC và qua C vẽ đường thẳng c//AB. Các đường thẳng b và c cắt nhau tại A' và cắt đường thẳng a lần lượt tại C' và B'. Chứng minh rằng: ∆ABC và ∆A'B'C' có cùng một trọng tâm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
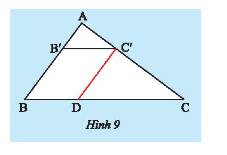
a) Xét tam giác \(ABC\) có \(B'C'//BC\) nên theo định lí Thales ta có:
\(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{2}{6} = \frac{{AC'}}{8}\). Do đó, \(AC' = \frac{{2.8}}{6} = \frac{8}{3}\left( {cm} \right)\).
Vậy \(AC' = \frac{{16}}{3}cm\).
b) Xét tam giác \(ABC\) có \(C'D//AB\) nên theo định lí Thales ta có:
\(\frac{{BD}}{{BC}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{{BD}}{{10}} = \frac{{\frac{8}{3}}}{8}\). Do đó, \(BD = \frac{{10.\frac{8}{3}}}{8} = \frac{{10}}{3}\left( {cm} \right)\).
Vậy \(BD = \frac{{10}}{3}cm\).
Ta có: \(BB' = AB - AB' = 6 - 2 = 4cm\)
Vì \(\left\{ \begin{array}{l}B'C'//BC\\C'D//AB\end{array} \right. \Rightarrow \left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right.\) (do \(D \in BC;B' \in AB\))
Xét tứ giác \(B'C'DB\) có
\(\left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right. \Rightarrow \) tứ giác \(B'C'DB\) là hình bình hành (dấu hiệu nhận biết)
\( \Rightarrow \left\{ \begin{array}{l}B'C' = BD = \frac{{10}}{3}cm\\BB' = C'D = 4cm\end{array} \right.\) (tính chất hình bình hành)
c) Ta có: \(\frac{{AB'}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AC'}}{{AC}} = \frac{{\frac{8}{3}}}{8} = \frac{1}{3};\frac{{BC'}}{{BC}} = \frac{{\frac{{10}}{3}}}{{10}} = \frac{1}{3}\)
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{{B'C'}}{{BC}}\).
18 tháng 7 2018
Ta có:
Tam giác ABC cân tại A => góc ABC = góc ACB
Mà góc ABD = góc ACD (=90độ) => góc ABD - góc ABC = góc ACD - góc ACB <=> góc DBC = góc DCB
=> Tam giác DBC cân ở D => DB=DC
b. gỌI I là giao điểm của AD và BC
Ta có: tam giác ABD = tam giác ACD (c-c-c)
=> góc BAD = góc CAD <=> góc BAI = góc CAI
=> tam giác BAI = tam giác CAI (c-g-c) => BI=IC
=> AI là trung trực của BC
CMTT có: DI là trung trực BC
=> Đường thẳng AD là trung trực của BC