Giups mình với ạ!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 10 2021
Bài 1:
\(a,=2\sqrt{3a}-5\sqrt{3a}+\dfrac{1}{2}\cdot4\sqrt{3a}=-3\sqrt{3a}+2\sqrt{3a}=-\sqrt{3a}\\ b,=\dfrac{a+b}{b^2}\cdot\dfrac{\left|a\right|b^2}{\left|a+b\right|}=\dfrac{a+b}{b^2}\cdot\dfrac{\left|a\right|b^2}{a+b}=\left|a\right|\\ c,=5\sqrt{a}-20\left|a\right|b\sqrt{a}+20a\left|b\right|\sqrt{a}-6\sqrt{a}\\ =\left(5\sqrt{a}-6\sqrt{a}\right)-\left(20ab\sqrt{a}-20ab\sqrt{a}\right)\\ =-\sqrt{a}\\ d,=\dfrac{\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)}{x+\sqrt{3}}=x-\sqrt{3}\\ e,=\dfrac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}{1-\sqrt{a}}=1+\sqrt{a}+a\)
Bài 2:
\(a,B=7\sqrt{x+2}-4\sqrt{x+2}-2\sqrt{x+2}=\sqrt{x+2}\\ b,ĐK:x\ge-2\\ PT\Leftrightarrow\sqrt{x+2}=20\Leftrightarrow x+2=400\Leftrightarrow x=398\left(tm\right)\)
Bài 3:
\(a,M=\dfrac{1+\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}=\dfrac{\sqrt{a}-1}{\sqrt{a}}\\ b,M=\dfrac{\sqrt{a}-1}{\sqrt{a}}=1-\dfrac{1}{\sqrt{a}}< 1\left(\dfrac{1}{\sqrt{a}}>0\right)\)
Giups mình với ạ
7 tháng 3 2022
Giúp gì vậy em! Có gì thì nêu câu hỏi ra nha! Không spam.
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 2 2022
\(P=-3\left(x^2+\dfrac{4}{9}y+\dfrac{64}{9}+\dfrac{4}{3}x\sqrt{y}-\dfrac{16}{3}x-\dfrac{32}{9}\sqrt{y}\right)-\dfrac{2}{3}\left(y-2y+1\right)+2022\)
\(P=-3\left(x+\dfrac{2\sqrt{y}}{3}-\dfrac{8}{3}\right)^2-\dfrac{2}{3}\left(\sqrt{y}-1\right)^2+2022\le2022\)
\(P_{max}=2022\) khi \(\left(x;y\right)=\left(2;1\right)\)
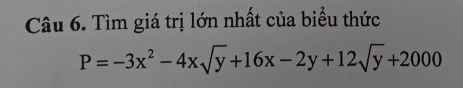
Xét tam giác ABC vuông tại A có AH là đường cao, ta có: \(AB^2=BH.BC=1.\left(1+4\right)=5\Rightarrow AB=\sqrt{5}cm\)
Áp dụng định lí Py-ta-go vào tam giác ABH vuông tại H có:
\(AB^2=BH^2+AH^2\Rightarrow AH^2=AB^2-BH^2=5-1=4\Rightarrow AH=2cm\)
Ta có: \(BC=BH+HC=1+4=5\left(cm\right).\)
Xét tam giác ABC vuông tại A, AH là đường cao (gt).
\(\Rightarrow AB^2=BH.BC\) (Hệ thức lượng).
\(\Rightarrow AB^2=1.5=5.\\ \Rightarrow AB=\sqrt{5}\left(cm\right).\)
\(AH^2=BH.CH\) (Hệ thức lượng).
\(\Rightarrow AH^2=1.4=4.\\ \Rightarrow AH=2\left(cm\right).\)