134 * 233 = ? không dùng máy tính ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Độ PH của mẫu 1 là:
\(a=-log\left[H^+\right]=-log\left[8\cdot10^{-7}\right]=-\left(log8-7\right)\)
\(=7-log8=7-log2^3=7-3\cdot log2\)
Độ PH của mẫu 2 là:
\(b=-log\left[2\cdot10^{-9}\right]=-\left(log2-9\right)=9-log2\)
\(a-b=7-3\cdot log2-9+log2=-2log2-2< 0\)
=>a<b
=>Độ PH của mẫu 2 lớn hơn

\(8^2=64=32+2\sqrt{16^2}\)
\(\left(\sqrt{15}+\sqrt{17}\right)^2=32+2\sqrt{15.17}=32+2\sqrt{\left(16-1\right)\left(16+1\right)}\)
\(=32+2\sqrt{16^2-1}\)
\(< =>8^2>\left(\sqrt{15}+\sqrt{17}\right)^2\)
\(8>\sqrt{15}+\sqrt{17}\)
\(\left(\sqrt{2019}+\sqrt{2021}\right)^2=4040+2\sqrt{2019.2021}\)
\(=4040+2\sqrt{\left(2020-1\right)\left(2020+1\right)}=4040+2\sqrt{2020^2-1}\)
\(\left(2\sqrt{2020}\right)^2=8080=4040+2\sqrt{2020^2}\)
\(< =>\sqrt{2019}+\sqrt{2021}< 2\sqrt{2020}\)
mik chọn điền
<
mik lười chép ại đề bài

Ta có: \(\sqrt{2,7}\cdot\sqrt{1,2}\)
\(=\sqrt{2,7\cdot1,2}\)
\(=\sqrt{\frac{27}{10}\cdot\frac{6}{5}}\)
\(=\sqrt{\frac{81}{25}}=\sqrt{\left(\frac{9}{5}\right)^2}=\frac{9}{5}\)
\(\sqrt{2,7}\cdot\sqrt{1,2}\)
\(=\sqrt{2,7\cdot1,2}\)
\(=\sqrt{\frac{27}{10}\cdot\frac{6}{5}}\)
\(=\sqrt{\frac{27}{5}\cdot\frac{3}{5}}\)
\(=\sqrt{\frac{81}{25}}\)
\(=\sqrt{\left(\frac{9}{5}\right)^2}\)
\(=\left|\frac{9}{5}\right|=\frac{9}{5}\)

a) 233 - 23 - 765 - 23 + 213
= (233 - 33 - 23 + 213) - 765
= 390 - 765
= -375
b) 41 + 243 - 344 + (-134)
= 41 + 243 - 344 - 134
= (41 + 243) - (344 + 134)
= 284 - 478
= -194

a. Có nhiều cách nhé. Với lớp 9 cô dùng cách này. Cô hướng dẫn nhé :)
Giả thiệt cho như hình vẽ. Gỉa sử AB = 1cm, khi đó do góc ADB = 30độ nên \(\frac{AB}{BD}=\frac{1}{2};\frac{AB}{AD}=\frac{\sqrt{3}}{3}\)
Vậy \(AC=AD+DC=AD+DB=2+\sqrt{3}\)
Vậy \(tan15=\frac{AB}{AC}=\frac{1}{2+\sqrt{3}}=2-\sqrt{3}\)
b. Dựa vào công thức : \(tan^215+1=\frac{1}{cos^215}\)

\(\frac{\sqrt{13,5}}{\sqrt{4,5}}=\sqrt{\frac{13,5}{4,5}}=\sqrt{3}\)
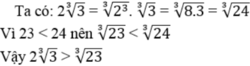

31222 do
31222