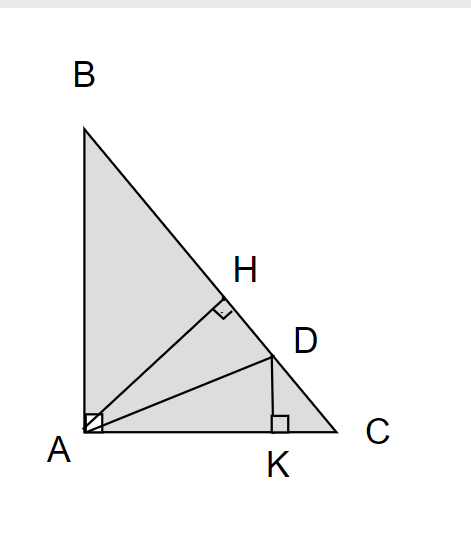
Cho tam giác ABC vuông tại A, đường cao AH. Trên cạnh BC lấy điểm D sao cho BD = BA. Đường vuông góc với BC tai D cắt AC ở E
a) So sánh AE và DE
b) Chứng minh AD là tia phân giác của góc HAC
c) Vẽ DK vuông góc với AC tại K. Chứng minh rằng AK = AH
d) Chứng minh rằng AB +AC < BC + AH