Tìm đa thức B , biết ;
Tổng của đa thức B với đa thức \(\left(4x^2y+5y^2-3xz+z^2\right)\) là 1 tổng đa thức không chức biến x.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 9 2023
a) Ta có:
B = (A + B) – A
= (x3 + 3x + 1) – (x4 + x3 – 2x – 2)
= x3 + 3x + 1 – x4 - x3 + 2x + 2
= – x4 + (x3 – x3) + (3x + 2x) + (1 + 2)
= – x4 + 5x + 3.
b) C = A - (A – C)
= x4 + x3 – 2x – 2 – x5
= – x5 + x4 + x3 – 2x – 2.
c) D = (2x2 – 3) . A
= (2x2 – 3) . (x4 + x3 – 2x – 2)
= 2x2 . (x4 + x3 – 2x – 2) + (-3) .(x4 + x3 – 2x – 2)
= 2x2 . x4 + 2x2 . x3 + 2x2 . (-2x) + 2x2 . (-2) + (-3). x4 + (-3) . x3 + (-3). (-2x) + (-3). (-2)
= 2x6 + 2x5 – 4x3 – 4x2 – 3x4 – 3x3 + 6x + 6
= 2x6 + 2x5 – 3x4 + (-4x3 – 3x3) – 4x2+ 6x + 6
= 2x6 + 2x5 – 3x4 – 7x3 – 4x2+ 6x + 6.
d) P = A : (x+1) = (x4 + x3 – 2x – 2) : (x + 1)
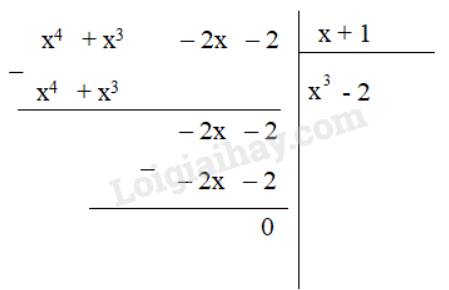
Vậy P = x3 - 2
e) Q = A : (x2 + 1)
Nếu A chia cho đa thức x2 + 1 không dư thì có một đa thức Q thỏa mãn
Ta thực hiện phép chia (x4 + x3 – 2x – 2) : (x2 + 1)
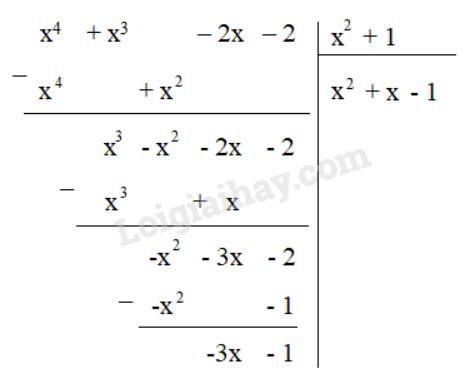
Do phép chia có dư nên không tồn tại đa thức Q thỏa mãn
NH
1
AH
Akai Haruma
Giáo viên
18 tháng 11 2021
Lời giải:
Ta có:
$A(x)=2x^3-7x^2-8x-4$
$=2x^2(x-2)-3x(x-2)-14(x-2)-32$
$=(x-2)(2x^2-3x-14)-32$
$=B(x)(2x^2-3x-14)-32$
Vậy đa thức thương là $2x^2-3x-14$
H9
HT.Phong (9A5)
CTVHS
2 tháng 8 2023
a) \(A=-11x^5+4x-12x^2+11x^5+13x^2-7x+2\)
\(A=\left(-11x^5+11x^5\right)+\left(-12x^2+13x^2\right)+\left(4x-7x\right)+2\)
\(A=0+x^2+\left(-3x\right)+2\)
\(A=x^2-3x+2\)
Bậc của đa thức là: \(2\)
Hệ số cao nhất là: \(1\)
b) Ta có: \(M\left(x\right)=A\left(x\right)\cdot B\left(x\right)\)
\(\Rightarrow M\left(x\right)=\left(x^2-3x+2\right)\cdot\left(x-1\right)\)
\(\Rightarrow M\left(x\right)=x^3-x^2-3x^2+3x+2x-2\)
\(\Rightarrow M\left(x\right)=x^3-4x^2+5x-2\)
c) A(x) có nghiệm khi:
\(A\left(x\right)=0\)
\(\Rightarrow x^2-3x+2=0\)
\(\Rightarrow x^2-x-2x+2=0\)
\(\Rightarrow x\left(x-1\right)-2\left(x-1\right)=0\)
\(\Rightarrow\left(x-1\right)\left(x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-1=0\\x-2=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
HP
1
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
a.
\(P-\left(5x^4-xyz\right)=xy+2x^4-6xyz+654\)
\(\Rightarrow P=5x^4-xyz+xy+2x^4-6xyz+654\)
\(\Rightarrow P=7x^4-7xyz+xy+654\)
b.
\(x^2-2x=0\)
\(\Leftrightarrow x\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)