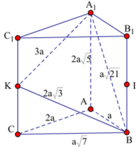
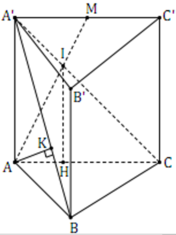
Cho lăng trụ đứng ABCA1B1C1 có AB = a, AC = 2a, AA = 2a\(\sqrt{5}\) và \(\widehat{BAC}=120^0\) Gọi M là trung điểm của CC1. CM \(MB\perp MA_1\) và tính khoảng cách từ điểm A đến mặt phẳng \(\left(A_1BM\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 7 2018
Đáp án D
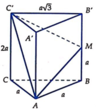
Nhận thấy ∆ A B C là hình chiếu của ∆ A M C ' lên mặt phẳng (ABC).
Gọi φ là góc giữa (AMC') và ( A B C ) ⇒ S ∆ A B C = S ∆ A M C ' . cos φ ⇒ cos φ = S ∆ A B C S ∆ A M C '
Ta có S ∆ A B C = 1 2 a 2 . sin 120 ° = a 2 3 4
A ' C = a 5 ; A M = a 2 ; B C = a 2 + a 2 - 2 a cos 120 ° = a 3 ⇒ C ' M = 2 a
Đặt p = a 5 + a 2 + 2 a 2
⇒ S ∆ A M C ' = p ( p - a 2 ) ( p - a 5 ) ( p - 2 a ) = 31 4 a 2
⇒
cos
φ
=
a
2
3
4
.
4
31
a
2
=
3
31
=
93
31
CM
20 tháng 12 2018
Đáp án B
Ta có:
S ∆ M N C = S ∆ A B C 4 = a 2 2 (đvdt).
⇒ V A ' M N C = 1 3 A A ' . S ∆ M N C = a 3 2 (đvtt).
Mặt khác: M N / / A B ⇒ M N ⊥ A C
Mà A A ' ⊥ m p ( A B C ) ⇒ M N ⊥ A A '
Do đó S ∆ A ' M N = 1 2 A ' M . M N = 1 2 A A ' 2 + A M 2 = a 10 2 2 (đvdt).
⇒ d ( C ; ( A ' M N ) ) = 3 V A ' M N C S ∆ A ' M N = 3 a 10 (đvđd).
CM
2 tháng 2 2017
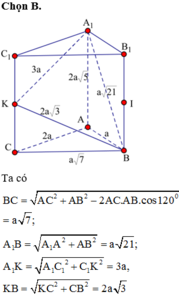
Chọn A
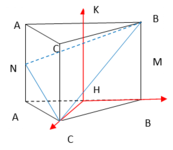
Gọi H, K lần lượt là là trung điểm cạnh A'B' và AB. Từ giả thiết ta có
Mặt khác: HC', HB' và HK đôi một vuông góc nhau.
Tọa độ hóa
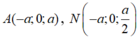
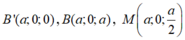
Xét mặt phẳng (BC'N) có
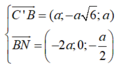
Phương trình (BC'N) là:
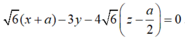
Khoảng cách từ M đến (BC'N) là:
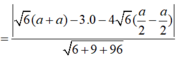
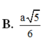
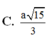
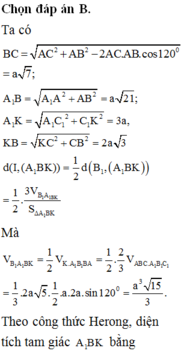
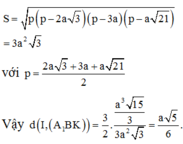
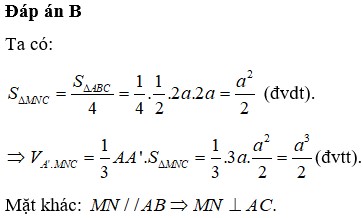
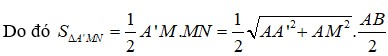
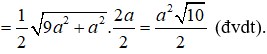
Đang thách thức mấy a/c CTV:))
=)) e chơi nx =))