Trong mặt phẳng với hệ tọa độ
Oxy, cho hai điểm A (2;0) , B (6;4). Viết phương trình đường tròn (C) tiếp xúc với trục hoành tại điểm A và khoảng cách từ tâm của (C) đến
điểm B bằng 5.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có n P → 1 ; 0 ; 0 ; n Q → 0 ; 1 ; − 1 suy ra n → = n P → ; n Q → = 0 ; 1 ; 1
Suy ra phương trình mặt phẳng cần tìm là: y + z − 5 = 0

Đáp án D
Ta có B A → = 3 ; 3 ; - 2 và (P) có véc tơ pháp tuyến n → = 1 ; - 3 ; 2 .
Gọi n ' → là véc tơ pháp tuyến của mặt phẳng (Q), để (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) thì: n → ⊥ n ' → ⊥ B A → ⇒ n ' = n → , B A → = 0 ; - 8 ; - 12 ⇒ Q : 0 x - 2 - 8 y - 4 - 12 z - 1 = 0 ⇔ 2 y + 3 z - 11 = 0

\(\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)=\left(3;-9\right)\)

Đáp án C
Phương pháp
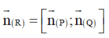
Cách giải: Ta có:
![]()
![]()
là 1 VTPT của mặt phẳng (R).
Vậy phương trình mặt phẳng (R):
![]()
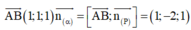
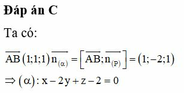
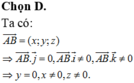
Trong mặt phẳng Oxy, cho hai điểm A(2;0) và B(6;4). Viết phương trình đường tròn (C) tiếp xúc với trục hoành tại A và khoảng cách từ tâm của (C) đến B bằng 5.
Gọi I(a;b) là tâm của đường tròn (C).
Vì đường tròn tiếp xúc với trục hoành tại A(2; 0) nên I(2;b) và R = b.
Phương trình đường tròn (C) có dạng: \(\left(x-2\right)^2+\left(y-b\right)^2=b^2\)
Trong mặt phẳng Oxy, cho hai điểm A(2;0) và B(6;4). Viết phương trình đường tròn (C) tiếp xúc với trục hoành tại A và khoảng cách từ tâm của (C) đến B bằng 5.
Gọi I(a;b) là tâm của đường tròn (C).
Vì đường tròn tiếp xúc với trục hoành tại A(2; 0) nên I(2;b) và R = b.
Khoảng cách từ B(6;4) đến tâm I(2;b) bằng 5 nên ta có:
\(IB=5\Rightarrow\sqrt{\left(2-6\right)^2+\left(b-4\right)^2}=5\)
\(\Rightarrow\left(2-6\right)^2+\left(b-4\right)^2=25\)
\(\Rightarrow16+\left(b-4\right)^2=25\)
\(\Rightarrow\left(b-4\right)^2=9\)
\(\Leftrightarrow\left[{}\begin{matrix}b-4=3\\b-4=-3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}b=7\\b=-1\end{matrix}\right.\)
Với b = 7, phương trình đường tròn (C) là \(\left(x-2\right)^2+\left(y-7\right)^2=49\)
Với b = 1, phương trình đường tròn (C) là \(\left(x-2\right)^2+\left(y-2\right)^2=1\)
Vậy phương trình đường tròn (C) là \(\left(x-2\right)^2+\left(y-7\right)^2=49\) hoặc \(\left(x-2\right)^2+\left(y-2\right)^2=1\)