Chứng minh rằng 6x^2+2 Không có nghiệm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NL
2
30 tháng 4 2015
ta có \(x^2+6x+10=x^2+6x+9+1=\left(x^2+6x+9\right)+1\)
\(=\left(x+3\right)^2+1\)
Vì \(\left(x+3\right)^2\ge0\)nên \(\left(x+3\right)^2+1\ge1\)
Vì \(\left(x+3\right)^2+1\ge1\)nên không có nghiệm
Vậy \(x^2+6x+10\)không có nghiệm
30 tháng 3 2018
\(x^2+6x+10\)
\(=x^2+3x+3x+3.3+1\)
\(=x\left(3+x\right)+3\left(3+x\right)+1\)
\(=\left(3+x\right)\left(3+x\right)+1\)
\(=\left(3x+1\right)^2+1\)
\(\text{Vi}:\left(3+x\right)^2\ge0\)
\(\Rightarrow\left(3+x\right)^2+x>1\)
=> Đa thức ko có nghiệm
6N
2
22 tháng 3 2022
\(-8^4+6x^3-4x^2+2x-1\)
Giả sử \(x\) là nghiệm nguyên
Trường hợp 1 (1)
\(-8^4+6x^3-4x^2+2x-1 \vdots x\)
\(=> 1 \vdots x => x= -1;1\)
Thay \(x\) bằng 1, -1. Ta thấy giá trị của biểu thức sau khi thay khác 0 nên 1 và -1 không phải là nghiệm
Trường hợp 2 : (2)
\(x=0\). Thay x thành 0 cho ra kết quả biểu thức khác không nên 0 không phải nghiệm
=> Từ (1) và (2) suy ra đpcm
27 tháng 3 2022
Bây giờ mình mới phát hiện là có phần bị khuất mất xin lỗi bạn
Trường hợp 1 (1)
Giả sử đa thức trên chia hết cho x
=> 1 chia hết cho x => x = 1 hoặc -1 (Lấy một ở cuối biểu thức nhe, lí do có phần suy ra này là bởi hiệu các số chia hết cho 1 số a bất kì sẽ chia hết cho số đó, áp dụng lại kiến thức học ở lớp 6)
Thay x thành 1 hoặc -1 ta được kết quả khác 0
Trường hợp 2 ...
26 tháng 1 2017
1023 chia hết cho 3 không chia hết cho 9
vt: Phải chia hết cho 3 => x=3t khi x=3t thì vế trái chia hết cho 9 => đpcm
6 tháng 4 2017
\(f\left(x\right)=-8x^4+6x^3-4x^2+2x-1\)
\(=-5x^4-\left(3x^4-6x^3+3x^2\right)-\left(x^2-2x+1\right)\)
\(=-5x^4-3\left(x^2-x\right)^2-\left(x-1\right)^2\le0\)
Mà ta dễ thấy dấu = không xảy ra nên f(x) không có nghiệm thuộc Z
PT
1
18 tháng 3 2016
Nhẩm nghiệm ta lấy ước của hệ số tự do đem chia cho 1
thay vào rồi thì sẽ biết
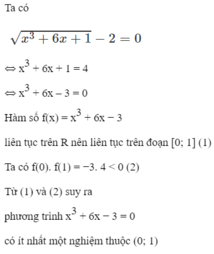
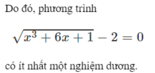
xét 6x^2+2=0
=> 6x^2=-2
ta có:x^2>/0 với mọi x thuộc R mà 6x^2<0
=> 6x^2+2 vô nghiệm
delta á