Đặt vật AB vuông góc với trục chính trước thấu kính phân kì cách thấu kính 50cm cho ảnh bằng 2/3 vật.
a)Tìm tiêu cự.
b)Dịch thấu kính như thế nào và một đoạn bằng bao nhiêu để thu được ảnh bằng 3/4 vật.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sơ đồ tạo ảnh:
![]()
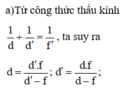
Số phóng đại ảnh qua thấu kính: k = − d ' d
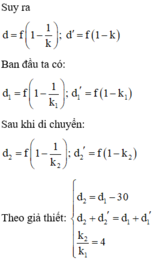
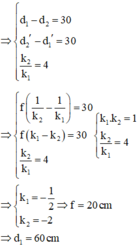
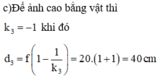
Như vậy để có ảnh cao bằng vật thì cần dịch chuyển vật lại gần thấu kính một đoạn 60 - 40 = 20 cm

Đáp án B
- Vì vật thật - ảnh thật nên
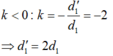
- Từ công thức thấu kính:
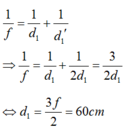
- Độ dịch chuyển của vật là:
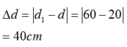

Tóm tắt:
d=25cm
Vì là ảnh thật => k <0 =-2
f=?
Giải
Có k=-d'/d
<=> -2 =-d'/25
=> d'= 50cm
f= d.d'/d+d' = 25*50/25+50=50/3 cm
Thấu kính này là thấu kính hội tụ
bạn có f =50/3cm, d=25cm, d'=50cm rồi bạn căn vở rồi vẽ thôi nhé
Câu 2: Tóm tắt
d=30cm
Giải
Cho 2 trường hợp
Trường hợp một k = 1/2 >0 là ảnh ảo
k=-d'/d
<=> 1/2 = -d'/30
=> d' = -15cm
f=d.d'/d+d' = 30*(-15)/30-15= -30 (Vô lý vì k >0 là ảnh ảo thì f <0, d<0)
Trường hợp 2
k=-1/2 là ảnh thật
k=-d'/d
<=> -1/2 = -d'/30
=> d' =15
f=d.d'/d+d' = 30*15/30+ 15= 10 ( hợp lí vì k<0 là ảnh thật và f>0, d>0)
Từ đó suy ra trường hợp 2 đúng và kết luận đây là thấu kính hội tụ
Vẽ hình bạn chỉ cần cho vật lớn hơn 2f là được (d>2f)

Ảnh ảo, cùng chiều và lớn hơn vật.
Ảnh cách thấu kính một đoạn:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{10}=\dfrac{1}{15}+\dfrac{1}{d'}\Rightarrow d'=30cm\)
Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{3}{h'}=\dfrac{15}{30}\Rightarrow h'=6cm\)

Chọn đáp án A.
Ta có d = 20 cm, ảnh thu được từ thấu kính phân kỳ là ảnh ảo có chiều cao bằng 1/2 lần vật nên d’ = -10cm. Mặt khác 1 f = 1 d + 1 d ' ⇒ f = − 20 c m .
Hình bạn tự vẽ nha:(
Gọi khoảng cách từ vật đến TK là: d
khoảng cách từ ảnh đến TK là: d"
chiều cao của vật là: h
chiều cao của ảnh là: h"
Xét △BOA ∼ △B"OA" ta có:
\(\dfrac{h}{h"}=\dfrac{d}{d"}\left(1\right)=\dfrac{3}{2}\) ➜d"=\(\dfrac{d.2}{3}\)= \(\dfrac{50.2}{3}\) ≃33cm
Xét △FIO ∼ △FB"A" ta có:
\(\dfrac{h}{h"}=\dfrac{f}{f-d"}\) (2)
Từ (1) và (2) ta có:
\(\dfrac{d}{d"}=\dfrac{f}{f-d"}\) Thay d= 50, d"= 33 ➜ f≃ 97
b) Cm tương tự ta có
\(\dfrac{h}{h"}=\dfrac{d}{d"}=\dfrac{4}{3}\) ➙d"= \(\dfrac{d.3}{4}\) (3)
tương tự ta có
\(\dfrac{d}{d"}=\dfrac{f}{f-d"}\) (4)
thay (3) vào (4) ta đc
\(\dfrac{d}{\dfrac{3.d}{4}}=\dfrac{f}{f-\dfrac{3.d}{4}}\)
Thay f= 97( tính ở phần a )➜d≃ 32