giải giúp mình câu 3 vs.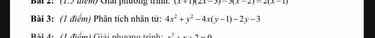
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ý C
\(\sqrt{\left(\left(xN-xM\right)^2+\left(yN-yM\right)^2\right)}\)·=\(\sqrt{\left(4-1\right)^2+\left(2+2\right)^2}\) = 5

3: góc AMN=góic ACM
=>AM là tiếp tuyến của đường tròn ngoại tiếp ΔECM
=>góc AMB=90 độ
=>Tâm o1 của đường tròn ngoại tiếp ΔECM nằm trên BM
NO1 min khi NO1=d(N;BM)
=>NO1 vuông góc BM
Gọi O1 là chân đường vuông góc kẻ từ N xuống BM
=>O1 là tâm đường tròn ngoại tiếp ΔECM có bán kính là O1M
=>d(N;tâm đường tròn ngoại tiếp ΔECM) nhỏ nhất khi C là giao của (O1;O1M) với (O) với O1 ;là hình chiếu vuông góc của N trên BM


Câu 2:
a, bạn tự vẽ được nhớ tìm tọa dộ nhé
x 0 0
y 0 0
b, Vì tung độ của điểm nằm trên P có hoành độ bằng 8
=> x = 8
Thay x = 8 vào y = 1/2x^2 ta được :
\(y=\dfrac{1}{2}.64=32\)
Bài 4:
a) Ta có: \(B=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}+1-\dfrac{2x+\sqrt{x}}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}\left(x\sqrt{x}+1\right)}{x-\sqrt{x}+1}+1-\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}\)
\(=\sqrt{x}\left(\sqrt{x}+1\right)+1-2\sqrt{x}-1\)
\(=x+\sqrt{x}-2\sqrt{x}\)
\(=x-\sqrt{x}\)

Gọi x là chiều cao của tam giác ; y là cạnh đáy của tam giác (x,y > 0 )
* chiều cao bằng 3/4 đáy:
x = 3/4y
=> x - 3/4y = 0 (1)
* Nếu chiều cao tăng thêm...tăng thêm 9m^2:
1/2(y-2)(x+3) = 1/2xy + 9 (sau đó bạn tự giải phương trình nha) (2)
Từ (1),(2) suy ra chiều cao là 12m , cạnh đáy là 16m


2:
b: Khi x=-3 thì (1) sẽ là -3(m-1)+2m+5=0
=>-3m+3+2m+5=0
=>8-m=0
=>m=8
c: Để ptvn thì m-1=0
=>m=1

18. iron-doing
19. wakes
còn lời giải chi tiết thì... mk ko biết .-.

3:
a: A(-3;1); B(2;4); C(3;1)
vecto BC=(1;-3)
=>AH có VTPT là (1;-3) và BC có VTPT là (3;1)
PT BC là:
3*(x-2)+1(y-4)=0
=>3x-6+y-4=0
=>3x+y-10=0
PT AH là;
1(x+3)-3(y-1)=0
=>x+3-3y+3=0
=>x-3y+6=0
vecto AC=(6;0)
=>BH có VTPT là (6;0)
Phương trình BH là;
6(x-2)=0
=>x=2
Tọa độ H là;
x=2 và x-3y+6=0
=>x=2 và 8-3y=0
=>H(2;8/3)
b: Tọa độ D là:
x-3y+6=0 và 3x+y-10=0
=>D(12/5;14/5)

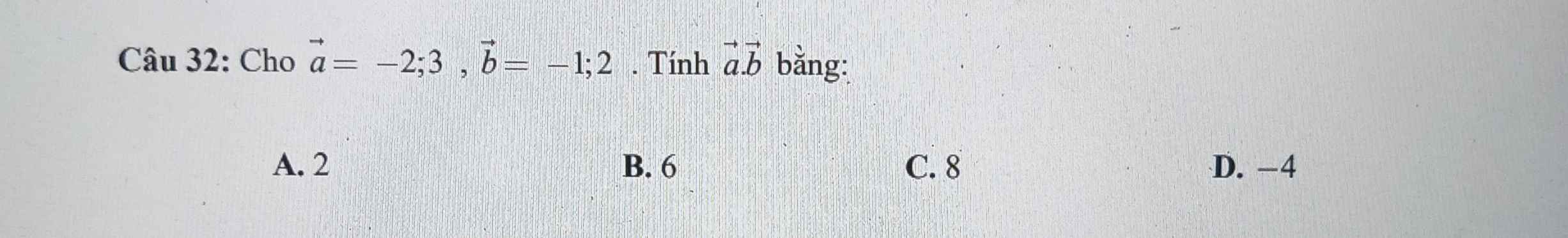
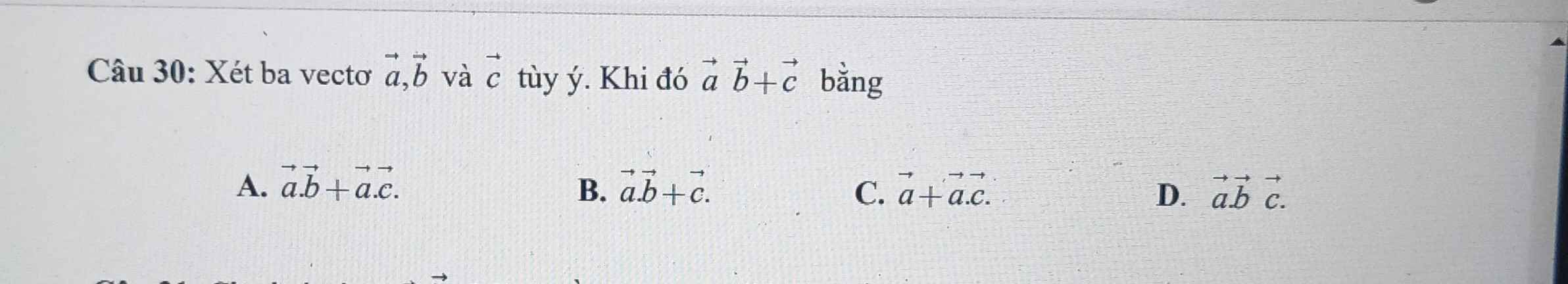


 mọi người giúp mình giải câu 2 3 4 và phần hình học vs ạ. mình cảm ơnnnnnnnnnnnnn
mọi người giúp mình giải câu 2 3 4 và phần hình học vs ạ. mình cảm ơnnnnnnnnnnnnn
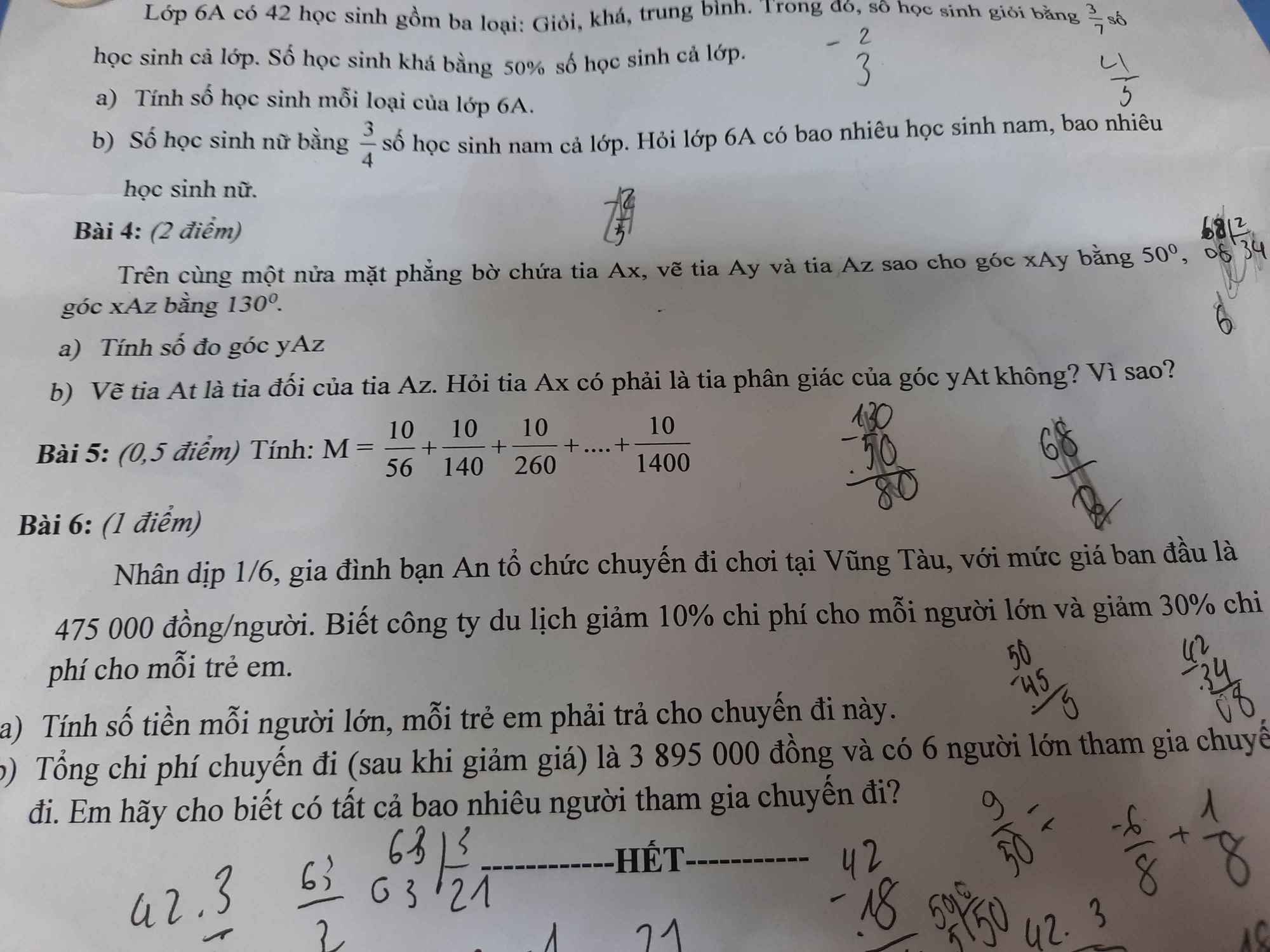



\(=4x^2-4xy+y^2+4x-2y-3\)
\(=\left(2x-y\right)^2+2\left(2x-y\right)-3\)
\(=\left(2x-y\right)^2-\left(2x-y\right)+3\left(2x-y\right)-3\)
\(=\left(2x-y-1\right)\left(2x-y\right)+3\left(2x-y-1\right)\)
\(=\left(2x-y-1\right)\left(2x-y+3\right)\)