Tìm m để hai đường thẳng (d1): 4x+4y=7 và (d2): 7x+3y=m cắt nhau tại một điểm trên trục Oy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
29 tháng 6 2023
(d1): 5x+4y=5
=>4y=-5x+5
=>y=-5/4x+5/4
(d2): 5x+2y=m
=>2y=-5x+m
=>y=-5/2x+m/2
Để hai đường cắt nhau tại trục Ox thì -5/4<>-5/2 và -5/4:(-5/4)=(-m/2):(-5/2)
=>\(-\dfrac{m}{2}\cdot\dfrac{2}{-5}=1\)
=>m=5
CM
13 tháng 2 2019
Giả sử hai đường thẳng ( d 1 ): 5x – 2y = 3; ( d 2 ): x + y = m cắt nhau tại điểm A(x, y).
Vì giao điểm A nằm trên trục Oy nên x = 0. Suy ra: A(0; y).
Khi đó điểm A(0; y) là nghiệm của hệ phương trình: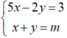 
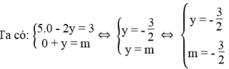
Vậy khi m = - 3/2 thì ( d 1 ): 5x – 2y = 3; (d2): x + y = m cắt nhau tại một điểm trên trục Oy.
Phương trình đường thẳng ( d 2 ): x + y = - 3/2
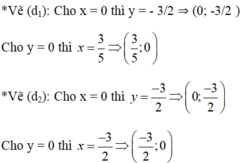
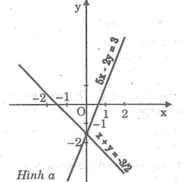
Đồ thị:
CM
9 tháng 1 2019
Giả sử hai đường thẳng ( d 1 ): mx + 3y = 10; ( d 2 ): x – 2y = 4 cắt nhau tại điểm B(x, y).
Vì điểm B nằm trên trục Ox nên y = 0 ⇒ B( x, 0).
Khi đó điểm B(x; 0) là nghiệm của hệ phương trình: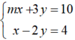 
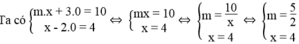
Vậy khi m = 5/2 thì ( d 1 ): mx + 3y = 10; ( d 2 ): x – 2y = 4 cắt nhau tại một điểm trên trục Ox.
Phương trình đường thẳng (d1):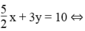
5x + 6y = 20
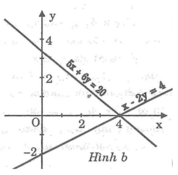
*Vẽ ( d 1 ): Cho x = 0 thì y = 10/3 ⇒ (0; 10/3 )
Cho y = 0 thì x = 4 ⇒ (4; 0)
*Vẽ ( d 2 ): x - 2y = 4. Cho x = 0 thì y = -2 ⇒ (0; -2)
Cho y = 0 thì x = 4 ⇒ (4; 0)
Đồ thị:
20 tháng 10 2021
a: Để (d1)//(d2) thì m+2=3m-2
\(\Leftrightarrow-2m=-4\)
hay m=2
AH
Akai Haruma
Giáo viên
11 tháng 1 2022
Lời giải:
Để hai đường thẳng song song nhau thì:
\(\left\{\begin{matrix} k+3=4\\ m+1\neq 3-m\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} k=1\\ m\neq 1\end{matrix}\right.\)
Để hai đt cắt nhau thì: \(\left\{\begin{matrix} k+3\neq 4\\ m\in\mathbb{R}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} k\neq 1\\ m\in\mathbb{R}\end{matrix}\right.\)
Để hai đt trùng nhau thì: \(\left\{\begin{matrix} k+3=4\\ m+1=3-m\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} k=1\\ m=1\end{matrix}\right.\)
Để hai đt cắt nhau tại 1 điểm trên trục tung thì:
PT hoành độ giao điểm $(k+3)x+m+1=4x+3-m$ nhận $x=0$ là nghiệm
$\Leftrightarrow x(k-1)+(2m-2)=0$ nhận $x=0$ là nghiệm
$\Leftrightarrow 2m-2=0$
$\Leftrightarrow m=1$
Vậy $m=1$ và $k\in\mathbb{R}$ bất kỳ.
Để 2 đt vuông góc thì $(k+3).4=-1$ và $m$ bất kỳ
$\Leftrightarrow k=\frac{-13}{4}$ và $m$ bất kỳ.
AH
Akai Haruma
Giáo viên
10 tháng 5 2021
Lời giải:
Giao điểm của 2 đường thẳng thuộc trục hoành nên có dạng $(a,0)$. Vì điểm này thuộc $(d_1):x+y=-1$ nên $a+0=-1\Rightarrow a=-1$
Vậy giao điểm của 2 ĐT trên là $(-1,0)$
Giao điểm này $\in (d_2)$ khi mà $m.(-1)+0=1$
$\Leftrightarrow m=-1$
18 tháng 2 2022
Phương trình hoành độ giao điểm là:
x-2m+1=2x-3
=>-x=-3+2m-1
=>-x=2m-4
=>x=-2m+4
Để hai đường thẳng cắt nhau tại một điểm nằm ở phía trên trục hoành thì y>0
=>2x-3>0
=>x>3/2