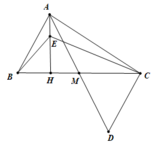
cho tam giác abc có ac>ab trung tuyến am . trên tia đối của tia ma lấy điểm d sao cho md=ma nối c với d
a. chứng minh góc adc> góc dac từ đó suy ra góc mab > góc mac
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
11 tháng 7 2018
Bn tự vẽ hình hộ mk nhé,còn lời giải thì(ns hướng làm thôi nha)
a,C/m tam giác AMB=DMC(cgc)
Nên AB=CD
Mà AB<AC(gt)
Nên CD<AC
\(\Rightarrow\)DAC<ADC(đpcm)
Có tam giác amb=dmc(cmt)
Nên MAB=MDC hay ADC
Mà ADC>DAC(cmt)
Nên MAB>MAC
b,Có tam giác abh vg,ahc vg
H là chân đg vg góc
MÀ AB<AC
Nên Hb<HC
LẠi có E\(\in\)AH nên EB<EC
hok tốt bài này vẽ ra là lm đc màk
CM
4 tháng 10 2018
b. Theo câu a, AB = CD mà AB < AC ⇒ CD < AC (0.5 điểm)
Trong tam giác ADC có CD < AC ⇒ ∠(DAC) < ∠(ADC) (0.5 điểm)
Mà ∠(BAM) = ∠(ADC) ( 2 góc tương ứng vì ΔABM = ΔDCM)
Suy ra (MAB) > (MAC) (0.5 điểm)
13 tháng 7 2016
Minh tự vẽ hình nhé!
a./ Xét \(\Delta MAB\)và \(\Delta MDC\)có:
- MB = MC (AM là trung tuyến nên M là trung điểm BC)
- góc AMB = góc DMC (đối đỉnh)
- MA = MD (gt)
=> \(\Delta MAB=\Delta MDC\)(cgc) => góc BAM = góc CDM (góc tương ứng); và CD = AB < AC (gt)
Trong \(\Delta ADC\)có AC < CD => góc ADC > góc DAC (góc đối diện với cạnh lớn hơn thì lớn hơn) đpcm 1.
vì \(\Delta MAB=\Delta MDC\) ta cũng => góc MAB = góc ADC > góc MAC . đpcm 2.
b./ AH vuông với BC tại H
=> H là hình chiếu của điểm A trên BC
và HB là hình chiếu tương ứng của đường xiên AB
HC là hình chiếu tương ứng của đường xiên AC
mà AB < AC => HB < HC ( đường xiên nhỏ hơn thì hình chiếu nhỏ hơn). đpcm 3
Mặt khác E thuộc AH => HB cũng là hình chiếu của đường xiên EB;
HC là hình chiếu của đường xiên EC
mà HB < HC (đpcm 3) => EC > EB (hình chiếu lớn hơn thì đường xiên lớn hơn) đpcm 4.