(1đ) Cho ABC vuông tại A. M là trung điểm của BC. Biết BC 10 (cm) Iét Mike MẸ vuông góc AB tại E (E = AB) và MF vuông góc AC tại F (F = AC) a) Về hình, chỉ giả thiết kết luận
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
20 tháng 1 2022
a,
GT KL tự làm
b, AM=1/2BC=5cm
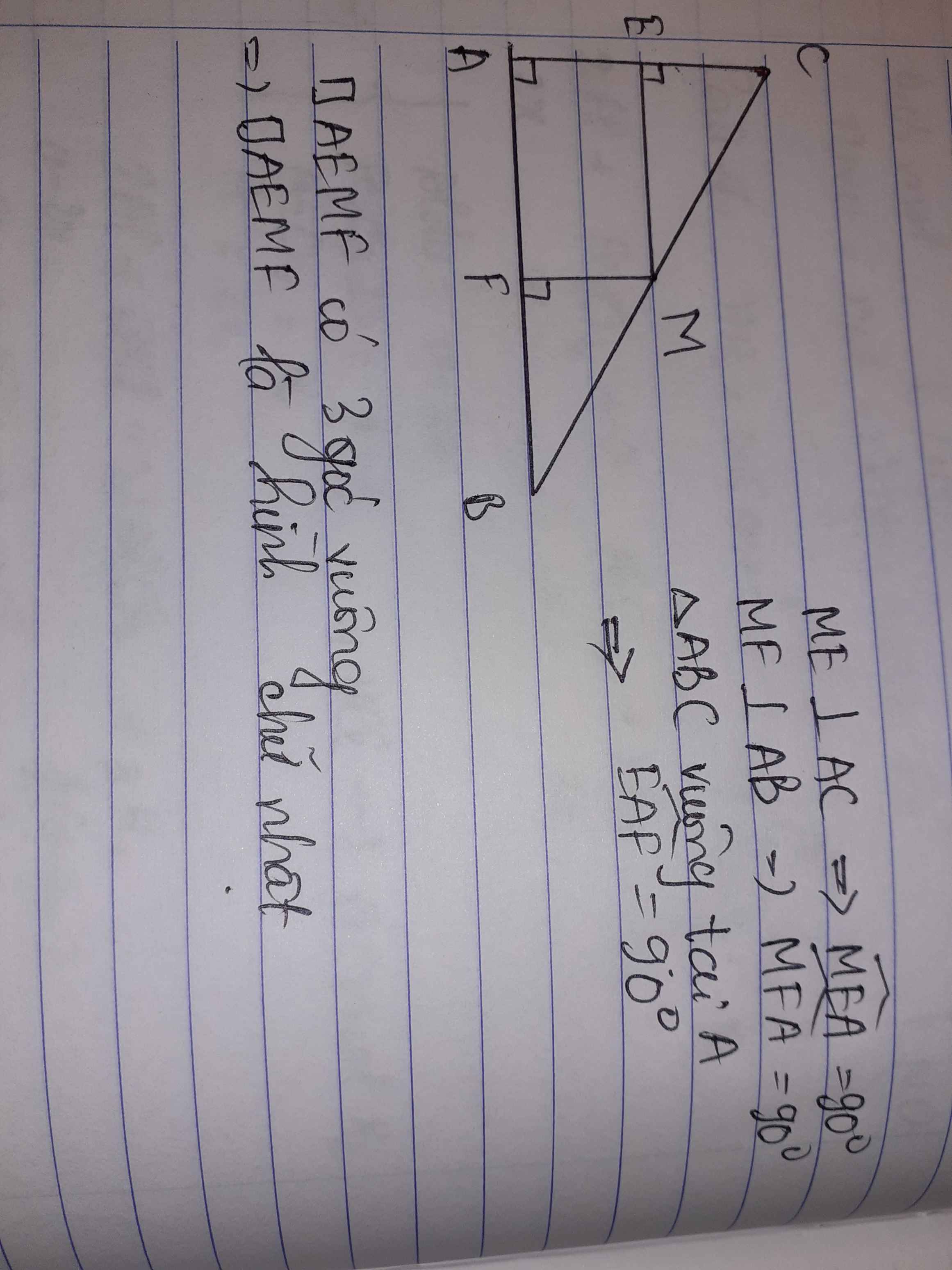
c,Xét tứ giác AEMF có 3 góc :\(MEA=EAF=AFM=90^o\)
do đó đó AEMF là hình chữ nhật
23 tháng 11 2021
Ta có AB vuông góc với AC, MF vuông góc với AC suy ra MF song song với AB, xét tam giácBca có m là trung điểm của BC, MF song song với AB suy ra ra f là trung điểm của AC mà f là trung điểm của mn suy ra m n cắt AC tại f suy ra tứ giác mcna là hình bình hành
13 tháng 7 2021
Xét tứ giác AFME có
\(\widehat{EAF}=90^0\)
\(\widehat{AEM}=90^0\)
\(\widehat{AFM}=90^0\)
Do đó: AFME là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
30 tháng 10 2023
Ta có; ΔABC vuông cân tại C
mà CD là đường trung tuyến
nên CD\(\perp\)AB và CD là phân giác của \(\widehat{ACB}\)
=>\(\widehat{ACD}=\widehat{BCD}=\dfrac{90^0}{2}=45^0\)
Gọi O là giao điểm của CM với FE
Xét tứ giác CEMF có
\(\widehat{CEM}=\widehat{CFM}=\widehat{FCE}=90^0\)
=>CEMF là hình chữ nhật
=>CM cắt EF tại trung điểm của mỗi đường và CM=EF
=>O là trung điểm chung của CM và EF và CM=EF
=>OM=OC=OE=OF
=>O là tâm đường tròn ngoại tiếp tứ giác CFME
\(\widehat{CEM}=\widehat{CFM}=\widehat{CDM}=90^0\)
Do đó: C,E,M,F,D cùng thuộc đường tròn đường kính CM
=>C,E,M,F,D cùng thuộc (O)
=>D thuộc (O)
Xét (O) có
ΔDFE nội tiếp
FE là đường kính
Do đó: ΔDFE vuông tại D
Xét tứ giác FDEC có
\(\widehat{FCE}+\widehat{FDE}=180^0\)
=>FDEC là tứ giác nội tiếp
=>\(\widehat{DFE}=\widehat{DCE}=\widehat{DCA}=45^0\)
Xét ΔDFE vuông tại D có \(\widehat{DFE}=45^0\)
nên ΔDFE vuông cân tại D
18 tháng 12 2022
a: Xét ΔFBC vuông tại F và ΔECB vuông tại E có
BC chung
góc FBC=góc ECB
Do đó: ΔFBC=ΔECB
=>CF=EB
b: Xét ΔMBC có góc MBC=góc MCB
nên ΔMCB cân tại M
=>MB=MC
mà AB=AC
nên AM là trung trực của BC
Đề bài yêu cầu gì?