Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔDBH vuông tại H và ΔECK vuông tại K có
DB=CE
góc DBH=góc ECK
=>ΔDBH=ΔECK
=>HB=CK
b: Xet ΔABH và ΔACK có
AB=AC
góc ABH=góc ACK
BH=CK
=>ΔABH=ΔACK
=>góc AHB=góc AKC
c: Xét ΔADE có AB/BD=AC/CE
nên BC//DE
=>HK//ED
d: Xét ΔAHE và ΔAKD có
AH=AK
HE=KD
AE=AD
=>ΔAHE=ΔAKD
a: Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE
\(\widehat{HBD}=\widehat{KCE}\)
Do đó: ΔHBD=ΔKCE
Suy ra: HB=KC
b: Xét ΔAHB và ΔAKC có
AB=AC
\(\widehat{ABH}=\widehat{ACK}\)
BH=CK
Do đó: ΔAHB=ΔAKC
Suy ra: \(\widehat{AHB}=\widehat{AKC}\)
c: Xét ΔADE có AB/AD=AC/AE
nên BD//ED
hay DE//HK
b) Ta có: \(\widehat{ABC}=\widehat{DBH}\)(hai góc đối đỉnh)
\(\widehat{ACB}=\widehat{ECK}\)(hai góc đối đỉnh
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{DBH}=\widehat{ECK}\)
Xét ΔDBH vuông tại H và ΔECK vuông tại K có
DB=CE(gt)
\(\widehat{DBH}=\widehat{ECK}\)
Do đó: ΔDBH=ΔECK
Suy ra: BH=CK
a)a) Xét ΔABCΔABC cân tại AA có:
- AB=ACAB=AC
- ˆABC=ˆACBABC^=ACB^
Lại có: ˆABC=ˆHBD,ˆACB=ˆKCEABC^=HBD^,ACB^=KCE^ (vì là các góc đối đỉnh)
⇒ˆHBD=ˆKCE.⇒HBD^=KCE^.
Xét ΔBHDΔBHD và ΔCKEΔCKE có:
- BD=CEBD=CE(gt)(gt)
- ˆHBD=ˆKCEHBD^=KCE^ (cmt)(cmt)
- ˆDHB=ˆEKC=900DHB^=EKC^=900(gt)(gt)
⇒ΔBHD=ΔCKE(ch−gn)⇒ΔBHD=ΔCKE(ch-gn)
⇒BH=CK(dpcm)⇒BH=CK(dpcm)
Vậy HB=CK.HB=CK.
b)b) Xét ΔABHΔABH và ΔACKΔACK có:
- AB=ACAB=AC (gt)(gt)
- BH=CKBH=CK (cmt)(cmt)
- ˆABH=ˆACKABH^=ACK^ (cùng bù với hai góc bằng nhau là: ˆABCABC^ và ˆACBACB^)
⇒ΔABH=ΔACK(c−g−c)⇒ΔABH=ΔACK(c-g-c)
⇒ˆAHB=ˆAKC,ˆBAH=ˆCAK.⇒AHB^=AKC^,BAH^=CAK^. (hai góc tương ứng)
Vậy ˆAHB=ˆAKC(dpcm).AHB^=AKC^(dpcm).
c)c) Xét ΔABCΔABC cân tại AA có:
⇒ˆABC=ˆACB=1800−ˆCAB2⇒ABC^=ACB^=1800-CAB^2
Ta có: AB=AC,BD=CEAB=AC,BD=CE
⇒AB+BD=AC+CE⇒AB+BD=AC+CE
⇔AD=AE.⇔AD=AE.
⇒ΔADE⇒ΔADE cân tại AA
⇒ˆADE=ˆAED=1800−ˆCAB2⇒ADE^=AED^=1800-CAB^2
Có: ˆADE=ˆABC,ˆACB=ˆAED(=1800−ˆCAB2)ADE^=ABC^,ACB^=AED^(=1800-CAB^2)
Mà các góc ở vị trí đồng vị.
⇒BC//ED⇒BC//ED. Mà H∈BC,K∈BCH∈BC,K∈BC
⇒HK//ED.⇒HK//ED.
Vậy ⇒HK//ED(dpcm).⇒HK//ED(dpcm).
d)d) Có ˆBAH=ˆCAKBAH^=CAK^(cmt)(cmt)
⇒ˆBAH+ˆBAE=ˆCAK+ˆBAE⇒BAH^+BAE^=CAK^+BAE^
⇔ˆHAE=ˆKAD.⇔HAE^=KAD^.
Xét ΔAHEΔAHE và ΔAKDΔAKD có:
- ˆHAE=ˆKADHAE^=KAD^ (cmt)(cmt)
- AH=AKAH=AK (do ΔABH=ΔACKΔABH=ΔACK(cmt)(cmt))
- AD=AEAD=AE (cmt)(cmt)
⇒ΔAHE=ΔAKD(c−g−c)⇒ΔAHE=ΔAKD(c-g-c)
Vậy ΔAHE=ΔAKD(dpcm).ΔAHE=ΔAKD(dpcm).
e)e) Có: ΔAHE=ΔAKDΔAHE=ΔAKD(cmt)(cmt)
⇒ˆAEH=ˆADK⇒AEH^=ADK^ (hai góc tương ứng)
Mà: ˆHDB=ˆKECHDB^=KEC^(cmt)(cmt)
⇒ˆAEH+ˆKEC=ˆADK+ˆHDB⇒AEH^+KEC^=ADK^+HDB^
⇔ˆHDI=ˆKEI⇔HDI^=KEI^
Mà: HD⊥BC,EK⊥BCHD⊥BC,EK⊥BC⇒HD//EK⇒HD//EK
⇒ˆHDI=ˆIKE⇒HDI^=IKE^ (hai góc so le trong)
⇒ˆDHI=ˆIEK⇒DHI^=IEK^ (hai góc so le trong)
⇒ˆHDI=ˆKEI=ˆIKE=ˆDHI⇒HDI^=KEI^=IKE^=DHI^
⇒ΔHID⇒ΔHID cân tại II, ΔKIEΔKIE cân tại II.
⇒HI=ID,IK=IE.⇒HI=ID,IK=IE.
Xét ΔHIDΔHID và ΔEIKΔEIK có:
-HD=EKHD=EK (cmt)(cmt)
-ˆHDI=ˆIKEHDI^=IKE^ (cmt)(cmt)
-ˆDHI=ˆIEKDHI^=IEK^(cmt)(cmt)
⇒ΔHID=ΔEIK(g−c−g)⇒ΔHID=ΔEIK(g-c-g)
⇒ID=IK, IH=IE.⇒ID=IK, IH=IE. (hai cạnh tương ứng)
Lại có: HI=ID,IK=IE.HI=ID,IK=IE.(cmt)(cmt)
⇒ID=IK=IH=IE⇒ID=IK=IH=IE
⇒ΔIED⇒ΔIED cân tại I⇔ID=IE.I⇔ID=IE.
⇒I⇒I thuộc đường trung trực của DEDE
Lại có: AD=AEAD=AE (ΔADEΔADE cân tại AA(cmt)(cmt))
⇒A⇒A thuộc đường trung trực của DEDE
⇒AI⇒AI là đường trung trực của DE.DE.
⇒AI⊥DE.⇒AI⊥DE.
Vậy AI⊥DEAI⊥DE(dpcm)(dpcm).
Hình tham khảo:
Chúc bạn học tốt .
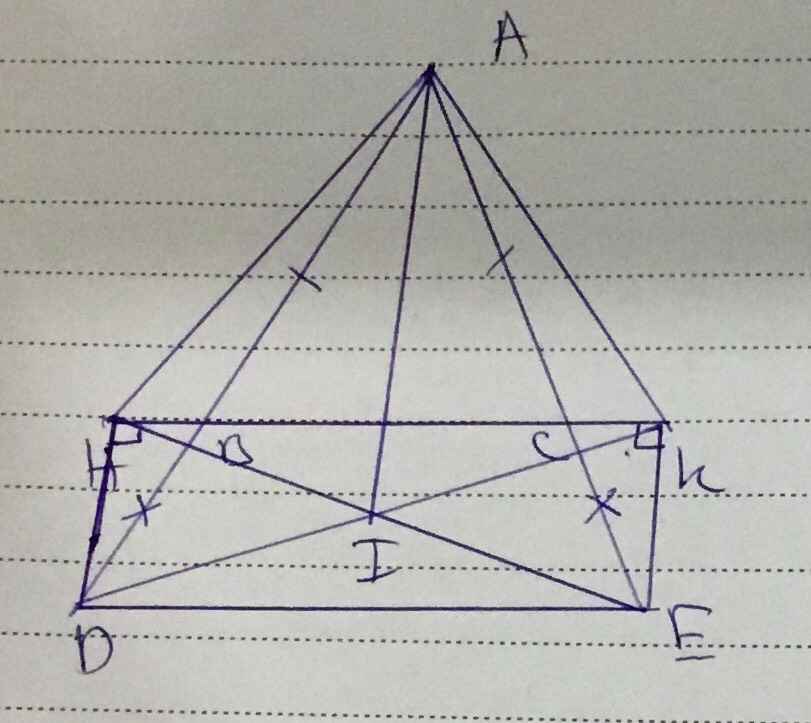
cho tam giác ABC cân ở a . trên tia đối của tia BA lấy điểm D , trên tia đối của tia CA lấy điểm E sao cho BD=CE . từ các điểm d và e lần lượt kẻ các đoạn thẳng DH, EK vuông góc với bc . c,m
a) BH=CK
b) tam giác ahk là tam giác cân
Tự vẽ hình nhá :)
AD = AB + BD
AE = AC + CE
Mà AB = AC ( \(\Delta ABC\)cân tại A )
BD = CE ( gt )
=> AD = AE
\(\widehat{HAE}=\widehat{HAB}+\widehat{BAE}\)
\(\widehat{KAD}=\widehat{KAC}+\widehat{CAD}\)
Mà \(\widehat{HAB}=\widehat{KAC}\) \(\left(\Delta ABH=\Delta AKC\right)\)
\(\Rightarrow\widehat{HAE}=\widehat{KAD}\)
Xét \(\Delta AHE\)và \(\Delta AKD\) có :
AD = AE ( cmt )
\(\widehat{HAE}=\widehat{KAD}\left(cmt\right)\)
AH = AK ( \(\Delta AHB=\Delta AKC\))
\(\Rightarrow\Delta AHE=\Delta AKD\left(c-g-c\right)\)