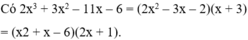Cho 2 phân thức:\(\frac{1}{x^2+ax-2}\) và \(\frac{2}{x^2+5x+b}\). Hãy xác định a, b biết rằng khi quy đồng mẫu thức chúng trở thành những phân thức có mẫu thức chung \(x^3+4x^2+x-6\).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 12 2018
Ta có mẫu thức chung phải chia hết cho từng mẫu thức riêng.
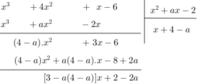
Vì phép chia này là phép chia hết nên số dư phải bằng 0, tức là:
3 – a(4 – a) = 0 và 2 – 2a = 0 ⇒ a = 1.
Vậy phân thức thứ nhất là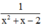 
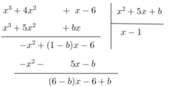
Vì phép chia này là phép chia hết nên số dư phải bằng 0, tức là:
6 – b = 0 và -6 + b = 0 ⇒ b = 6.
Vậy phân thức thứ hai là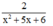 
* Quy đồng:
ND
Nguyễn Đức Trí
VIP
21 tháng 9 2023
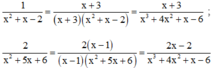
a) \(\dfrac{1}{x-a};\dfrac{2}{x-b}\)
Theo đề bài ta có :
\(\left(x-a\right)\left(x-b\right)=x^2-5x+6\)
\(\Leftrightarrow\left(x-a\right)\left(x-b\right)=\left(x-2\right)\left(x-3\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\)
b) \(\dfrac{1}{x-a}=\dfrac{1}{x-2}=\dfrac{x-3}{\left(x-2\right)\left(x-3\right)}=\dfrac{x-3}{x^2-5x+6}\)
\(\dfrac{2}{x-b}=\dfrac{1}{x-3}=\dfrac{2\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}=\dfrac{2x-6}{x^2-5x+6}\)
