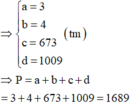Cho a,b,c,d là số nguyên biết a+b=c+d và c*d là các số nguyên liên tiếp .CMR c=d
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sử dụng quy tắc đa thức: \(P\left(a\right)-P\left(b\right)\) chia hết \(a-b\) cho đa thức hệ số nguyên
Do a;b;c;d lẻ nên hiệu của chúng đều chẵn
\(P\left(c\right)-P\left(a\right)=4\Rightarrow4⋮c-a\Rightarrow\left[{}\begin{matrix}c-a=-2\\c-a=-4\end{matrix}\right.\)
Tương tự ta có \(\left[{}\begin{matrix}b-a=-2\\b-a=-4\end{matrix}\right.\)
Mà \(a>b>c\) \(\Rightarrow b-a>c-a\Rightarrow\left[{}\begin{matrix}b-a=-2\\c-a=-4\end{matrix}\right.\)
\(\Rightarrow a;b;c\) là 3 số nguyên lẻ liên tiếp
Lại có \(P\left(b\right)-P\left(d\right)=4⋮b-d\Rightarrow b-d=\left\{-4;-2;2;4\right\}\)
Tương tự: \(c-d=\left\{-4;-2;2;4\right\}\) (1)
Do đã chứng minh được a; b và c là 2 số lẻ liên tiếp \(\Rightarrow c=b-2\) ; \(c=a-4\) (2)
- Nếu \(b-d=-4\Rightarrow c-d=b-2-d=-4-2=-6\) không thỏa mãn (1) (loại)
- Nếu \(b-d=-2\Rightarrow c-d=b-d-2=-4\) \(\Rightarrow c=d-4\)
\(\Rightarrow d=a\) theo (2) trái giả thiết a;b;c;d phân biệt (loại)
- Nếu \(b-d=2\Rightarrow c-d=b-d-2=0\Rightarrow c=d\) trái giả thiết c;d phân biệt (loại)
- Nếu \(b-d=4\Rightarrow c-d=b-d-2=2\)
\(\Rightarrow d\) là số lẻ liền trước của c
Vậy a;b;c;d là bốn số nguyên lẻ liên tiếp theo thứ tự \(a>b>c>d\)

2) \(a^2+b^2=c^2+d^2\)
\(\Leftrightarrow\left(a+b\right)^2-2ab=\left(c+d\right)^2-2cd\)
\(\Leftrightarrow\left(a+b\right)^2-\left(c+d\right)^2=2\left(ab-cd\right)\)
\(\Leftrightarrow\left(a+b+c+d\right)\left(a+b-c-d\right)=2\left(ab-cd\right)\)
Ta có \(\left(a+b+c+d\right)+\left(a+b-c-d\right)=2\left(a+b\right)\) là số chẵn
\(\Rightarrow\) \(\left(a+b+c+d\right)\) và \(\left(a+b-c-d\right)\) có cùng tính chẵn lẻ
Mặt khác \(\left(a+b+c+d\right)\left(a+b-c-d\right)=2\left(ab-cd\right)\) chia hết cho 2
Nên \(\left(a+b+c+d\right)\) và \(\left(a+b-c-d\right)\) ko thể cùng lẻ
\(\Rightarrow\) \(\left(a+b+c+d\right)\) và \(\left(a+b-c-d\right)\) cùng chẵn
Mà \(a+b+c+d>2\) nên \(a+b+c+d\) là hợp số.
 #hoktot#
#hoktot#