Giúp e bài này vs ạ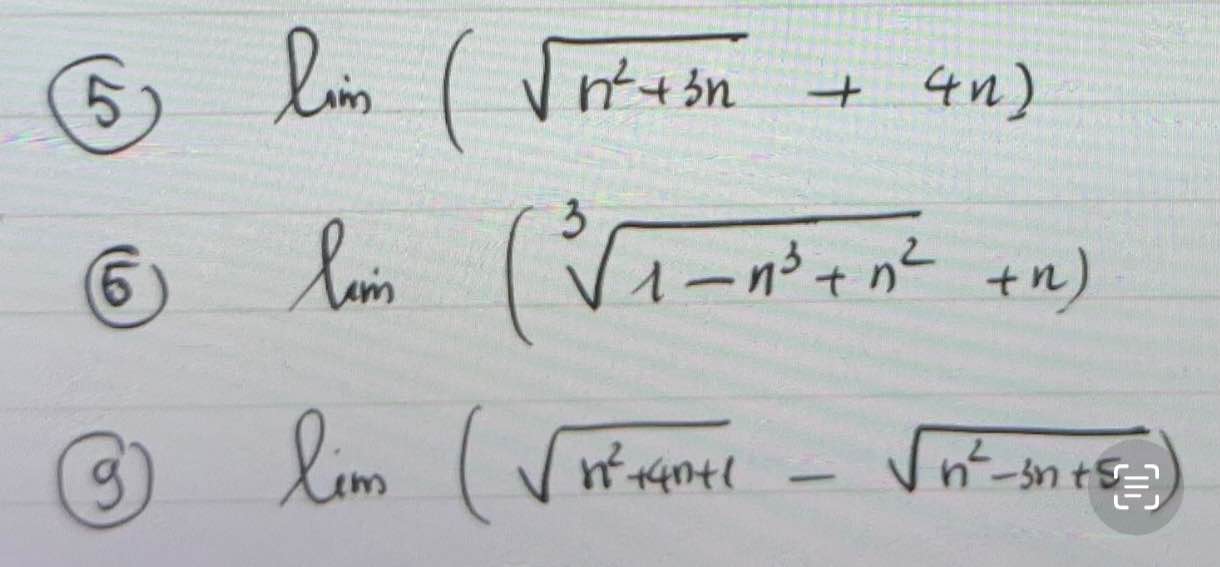
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 2 2022
Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
Mn giúp e bài này vs ạ , e cảm ơn nhìu ạ!
DT
Đỗ Thanh Hải
CTVVIP
9 tháng 4 2021
1 Last week the doctor advised him not to swim in a few weeks
2 William Shakespeare was born on April 23th, 1564
3 He was the eldest son of a wealthy glove maker
4 He got married to Anne Hathaway and had three children
5He moved to Lon don in 1588 and joined in a theatrical company
6 tháng 10 2021
Bài 5:
A[-2;10)
\(A\cup B=\left(-\infty;10\right)\)
\(A\cap B=\varnothing\)
A\B=[-2;10)
B\A=(-\(\infty\);-3)
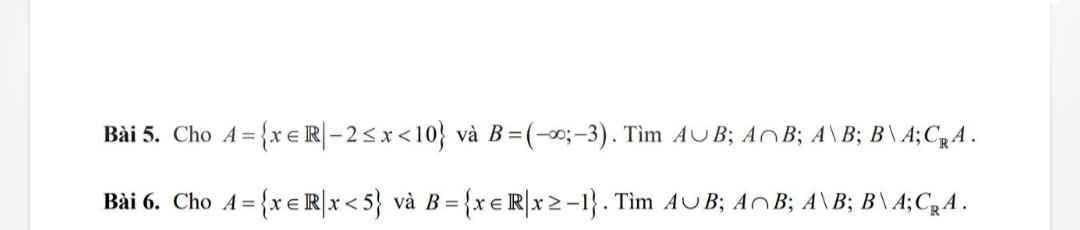
\(\lim\left(\sqrt{n^2+3n}+4n\right)=\lim n\left(\sqrt{1+\dfrac{3}{n}}+4\right)=+\infty\left(1+4\right)=+\infty\)
\(\lim\left(\sqrt[3]{1-n^3+n^2}+n\right)=\lim\dfrac{1+n^2}{\sqrt[3]{\left(1-n^3+n^2\right)^2}-n\sqrt[3]{1-n^3+n}+n^2}\)
\(=\lim\dfrac{\dfrac{1}{n^2}+1}{\sqrt[3]{\left(\dfrac{1}{n^3}-1+\dfrac{1}{n}\right)^2}-\sqrt[3]{\dfrac{1}{n^3}-1+\dfrac{1}{n^2}}+1}=\dfrac{1}{1-\left(-1\right)+1}=\dfrac{1}{3}\)
\(\lim\left(\sqrt[]{n^2+4n+1}-\sqrt[]{n^2-3n+5}\right)=\lim\dfrac{7n-4}{\sqrt[]{n^2+4n+1}+\sqrt[]{n^2-3n+5}}\)
\(=\lim\dfrac{7-\dfrac{4}{n}}{\sqrt[]{1+\dfrac{4}{n}+\dfrac{1}{n^2}}+\sqrt[]{1-\dfrac{3}{n}+\dfrac{5}{n^2}}}=\dfrac{7}{1+1}=\dfrac{7}{2}\)