a)Nếu x;y;z tỉ lệ thuận với a,b,c thì ta có? Nếu x;y;z tỉ lệ nghịch với a,b,c thì ta có? b) Cách tính giá trị của hàm số tại 1 giá trị cho trước của biển. c)Cách tìm giá trị của biến số khi biết giá trị của hàm số. d) Nếu điểm nằm trên đồ thị hàm số thì tọa độ của nó thỏa mãn công thức của hàm số. e) Cách kiểm tra một điểm có tọa độ cho trước có thuộc đồ thị hàm số không.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.khang dinh A,B,D dung
2,x-(1-x)=5+(-1+x)
x-1+x=5-1+x
2x-1=4+x
2x-x=4+1
x=5
Vay x=5
co bai kho hoi mik nhe

\(x=3,5\Rightarrow\left|x\right|=3,5\\ x=\dfrac{-4}{7}\Rightarrow\left|x\right|=\dfrac{4}{7}\\ x>0\Rightarrow\left|x\right|=x\\ x=0\Rightarrow\left|x\right|=0\\ x< 0\Rightarrow\left|x\right|=-x\)
a/ nếu x = 3,5 thì |x| = |3,5|
nếu x = -4/7 thì |x| = |-4/7|
b/ nếu x>0 thì |x|= x
nếu x=0 thì |x| = 0
nếu x <0 thì |x|= -x
CHÚC BẠN HỌC TỐT NHÁ THÚY NGÂN ...

Chọn đáp án C
Mệnh đề 1 và mệnh đề 3 đúng.
Mệnh đề 2 sai tại điều kiện x > y > 0 , sửa lại:
Nếu x > 0 , y > 0 và 0 < a ≠ 1 thì mệnh đề
![]()

Bài làm
a) Giả sử P(x) có một nghiệm là 1 thì:
p(1)=a*1^2+b*1+c
=a+b+c
Mà a+b+c=0
=>p(1)=0
=>đa thức p(x) có 1 nghiệm là 1(ĐPCM)
b)Giả sử P(x) có 1 nghiệm là -1 thì
p(-1)=a*(-1)^2+b*(-1)+c
=a-b+c
Mà a-b+c=0
=>p(-1)=0
=> đa thức p(x) có một nghiệm là -1(ĐPCM)
c)TA có:
p(1)=a*1^2+b*1+c=a+b+c
p(-1)=a.(-1)^2+b*(-1)+c=a-b+c
Mà p(1)=p(-1)
=>a+b+c=a-b+c
=>a+b+c-a+b-c=0
=>2b=0 =>b=0
+) Với b=0 =>p(x)=ax^2+c (1)
=>p(-x)=a*(-x)^2+c=a*x+c (2)
Từ (1)và (2) =>p(x)=p(-x) (ĐPCM)

Lời giải:
Nếu $x>0$ thì $-x< 0$. Do đó $-x< 0< x\Rightarrow -x< x$. Đáp án A sai
Nếu $x>0\Rightarrow -x< 0$. Đáp án B sai
Nếu $x< 0\Rightarrow -x>0$. Do đó $-x>0>x\Rightarrow -x>x$. Đáp án C sai
Nếu $x>0\Rightarrow -x< 0$. Đáp án D đúng (chọn)

B1
/x/=7=>x thuộc {-7;7}
/x/=2=> x thuộc {2;-2}
/x/<3=> x thuộc {-2;-1;0;1;2}
b2
Nếu /a/=a thì a>0
Nếu /a/=-a thì a<0
Nếu /a/>a thì a<0

TH1: Lấy \(x_1;x_2\in R\) sao cho \(0< x_1< x_2\)
\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{a\cdot\left(x_1^2-x_2^2\right)}{x_1-x_2}=a\cdot\left(x_1+x_2\right)\)>0 vì \(x_1+x_2>0;a>0\)
=>Hàm số y=f(x)=ax2 đồng biến khi x>0 nếu a>0
TH2: Lấy \(x_1;x_2\in R^+;0< x_1< x_2\)
\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{a\cdot\left(x_1^2-x_2^2\right)}{x_1-x_2}=\dfrac{a\left(x_1-x_2\right)\left(x_1+x_2\right)}{x_1-x_2}\)
\(=a\left(x_1+x_2\right)< 0\)(vì x1+x2>0 và a<0)
=>Hàm số nghịch biến khi x>0
TH3: Lấy \(x_1;x_2\in R^-\) sao cho \(x_1< x_2< 0\)
\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{a\left(x_1^2-x_2^2\right)}{x_1-x_2}=\dfrac{a\left(x_1+x_2\right)\left(x_1-x_2\right)}{x_1-x_2}\)
\(=a\left(x_1+x_2\right)>0\) vì a<0 và x1+x2<0
=>Hàm số đồng biến khi x<0
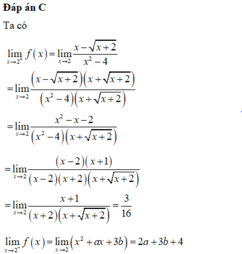
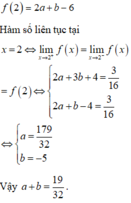
a: x,y,z tỉ lệ thuận với a,b,c
thì x/a=y/b=z/c
x,y,z tỉ lệ nghịch với a,b,c
nên ax=yb=cz
b: Chỉ cần thay giá trị của biến vào hàm số
c: Đặt hàm số có giá trị bằng giá trị cho trước xong rồi tìm giá trị của biến