Hình thang ABCD (AB<CD) có diện tích là 2008cm vuông.M là trung điểm của cạnh BC. Nối M với A và D. Tính diện tích tam giác AMD
nêu rõ cách làm giúp mình nhé mình sẽ hậu tạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

từ A hạ \(AE\perp DC\)
từ B hạ \(BF\perp DC\)
\(AB//CD=>AB//EF\)\(=>ABCD\) là hình chữ nhật
\(=>AB=EF=2cm\)
vì ABCD là hình thang cân\(=>\left\{{}\begin{matrix}AD=BC\\\angle\left(ADE\right)=\angle\left(BCF\right)\end{matrix}\right.\)
mà \(\angle\left(AED\right)=\angle\left(BFC\right)=90^o\)
\(=>\Delta ADE=\Delta BFC\left(ch.cgn\right)=>DE=FC=\dfrac{DC-EF}{2}=\dfrac{6-2}{2}=2cm\)
xét \(\Delta ADE\) vuông tại E có: \(AE=\sqrt{AD^2-ED^2}=\sqrt{3^2-2^2}=\sqrt{5}cm\)
\(=>S\left(ABCD\right)=\dfrac{\left(AB+CD\right)AE}{2}=\dfrac{\left(2+6\right)\sqrt{5}}{2}=4\sqrt{5}cm^2\)

Bài 1: △ABD=△BAC(c−g−c)△ABD=△BAC(c−g−c)
=>AC=BD=>AC=BD
△ACD=△BDC(c−c−c)△ACD=△BDC(c−c−c)
=>ADCˆ=BCDˆ=>ADC^=BCD^
Mà ADCˆ+DABˆ+ABCˆ+BCDˆ=360oADC^+DAB^+ABC^+BCD^=360o
=>2(DABˆ+ADCˆ)=360o=>2(DAB^+ADC^)=360o
=>DABˆ+ADCˆ=180o=>DAB^+ADC^=180o
=>AB//CD=>AB//CD
=>ABCD=>ABCD là hình thang mà có 2 góc ở đáy bằng nhau nên lf thang cân ![]()
Bài 4: chắc mấy bạn ở dưới vẽ sai hình :3 -_-
hình vẽ chính xác là ta vẽ được một hình thang cân với AD//BCAD//BC sẽ có được đầy đủ điều kiện đề bài đưa ra ![]()
Giải:
△ADB=△DAC△ADB=△DAC (c-c-c)
=>DABˆ=ADCˆ=>DAB^=ADC^
Từ đây chứng minh như câu 1 là =>đpcm ![]() )
)

Gợi ý: Kẻ AH ^ CD tại H, kẻ BK ^ CD tại K
Tính được SABCD = 180cm2

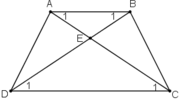
Gọi E là giao điểm của AC và BD.
+ 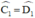 ⇒ ΔEDC cân tại E ⇒ ED = EC (1)
⇒ ΔEDC cân tại E ⇒ ED = EC (1)
+ AB//CD ⇒ 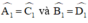 (Các cặp góc so le trong)
(Các cặp góc so le trong)
Mà 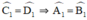
⇒ ΔEAB cân tại E ⇒ EA = EB (2)
Từ (1) và (2) suy ra: EA + EC = EB + ED hay AC = BD.
Vậy hình thang ABCD có hai đường chéo AC = BD nên là hình thang cân.