Cho biểu thức A=16x^2-1/16x^2-8x+1.
a)tìm ĐKXĐ
b)rút gọn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a.\)
\(\dfrac{16x^2-1}{16x^2-8x+1}\\ =\dfrac{\left(4x\right)^2-1}{\left(4x-1\right)^2}\\ =\dfrac{\left(4x-1\right)\left(4x+1\right)}{\left(4x-1\right)^2}\\ =\dfrac{4x+1}{4x-1}\)
\(b.\)
\(\dfrac{4x^2-4xy+y^2}{-\left(4x^2-y^2\right)}\\ =-\dfrac{\left(2x-y\right)^2}{\left(2x-y\right)\left(2x+y\right)}\\ =\dfrac{-\left(2x-y\right)}{2x+y}\\ =\dfrac{y-2x}{y+2x}\)
a) Ta có: \(\dfrac{16x^2-1}{16x^2-8x+1}\)
\(=\dfrac{\left(4x-1\right)\left(4x+1\right)}{\left(4x-1\right)^2}\)
\(=\dfrac{4x+1}{4x-1}\)
b) Ta có: \(\dfrac{4x^2-4xy+y^2}{y^2-4x^2}\)
\(=\dfrac{\left(2x-y\right)^2}{\left(y-2x\right)\left(y+2x\right)}\)
\(=\dfrac{\left(y-2x\right)^2}{\left(y-2x\right)\left(y+2x\right)}\)
\(=\dfrac{y-2x}{y+2x}\)

a) x ≠ -5.
b) Ta có P = ( x + 5 ) 2 x + 5 = x + 5
c) Ta có P = 1 Û x = -4 (TMĐK)
d) Ta có P = 0 Û x = -5 (loại). Do vậy x ∈ ∅ .

`đk:x-\sqrt{x^2-4x+4}>=0`
`<=>x>=\sqrt{x^2-4x+4}`
`<=>x^2>=x^2-4x+4(x>=0)`
`<=>4x-4>=0`
`<=>4x>=4<=>x>=1`
`b)A=sqrt{x-sqrt{(x-2)^2}}`
`=sqrt{x-|x-2|}`
`x>=2=>|x-2|=x-2`
`=>A=sqrt{x-x+2}=sqrt2`
`1<=x<=2=>|x-2|=2x-`
`=>A=\sqrt{x+x-2}=sqrt{2x-2}`

a) Rút gọn:
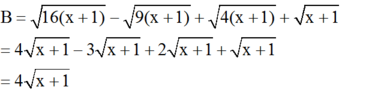
b) Để B = 16 thì:
![]()
⇔ x + 1 = 16 ⇔ x = 15 (thỏa mãn x ≥ -1)

a.
\(B=\sqrt{16x+16}-\sqrt{9x+9}+\sqrt{4x+4}+\sqrt{x+1}\left(x\ge-1\right)\)
\(B=\sqrt{16}.\sqrt{x+1}-\sqrt{9}.\sqrt{x+1}+\sqrt{4}.\sqrt{x+1}+\sqrt{x+1}\)
\(B=4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}\)
\(B=\left(4-3+2+1\right).\sqrt{x+1}\)
\(B=4.\sqrt{x+1}\)
b.
\(B=16\\\)
\(\Rightarrow4\sqrt{x+1}=16\)
\(\Rightarrow\sqrt{x+1}=\dfrac{16}{4}=4\)
\(\Rightarrow x+1=4^2\)
\(\Rightarrow x+1=16\rightarrow x=16-1=15\) (thỏa mãn)
vậy x=15

\(a,\left(2x-1\right)\left(4x^2+2x-1\right)-8x^3+16x\)
\(\Leftrightarrow\)\(8x^3+4x^2-2x-4x^2-2x+1-8x^3+16x\)
\(\Leftrightarrow\)\(4x^2-2x-4x^2-2x+1+16x\)
\(\Leftrightarrow12x+1\)
\(b,\left(x+2\right)^3-x^2\left(x+6\right)-2x-5\)
\(\Leftrightarrow x^3+6x^2+12x+8-x^3-6x^2-2x-5\)
\(\Leftrightarrow6x^2+12x+8-6x^2-2x-5\)
\(\Leftrightarrow10x+3\)
Mình cũng không biết đúng hay sai nữa :V
\(A=\dfrac{16x^2-1}{16x^2-8x+1}\)
\(=\dfrac{\left(4x-1\right)\left(4x+1\right)}{\left(4x-1\right)^2}\)
a) ĐKXĐ:
\(\left(4x-1\right)^2\ne0\Leftrightarrow4x-1\ne0\Leftrightarrow x\ne\dfrac{1}{4}\)
b) \(A=\dfrac{\left(4x+1\right)\left(4x-1\right)}{\left(4x-1\right)^2}=\dfrac{4x+1}{4x-1}\)
a,đkxđ : \(16x^2\ne0\Leftrightarrow x\ne0\)
b, \(\dfrac{16x^2}{1}-\dfrac{1}{16x^2}-\dfrac{8x}{1}+1=\dfrac{256x^4}{16x^2}-\dfrac{1}{16x^2}-\dfrac{128x^3}{16x^2}+\dfrac{16x^2}{16x^2}\)
\(=\dfrac{256x^4-1-128x^3+16x^2}{16x^2}=\dfrac{256x^4-128x^3+16x^2-1}{16x^2}\)
\(=\dfrac{\left(256x^4-128x^3+16^2\right)-1}{16x^2}=\dfrac{16x^2\left(16x^2-8x+1\right)-1}{16x^2}\)
\(=\dfrac{\left(4x\right)^2.\left(\left(4x\right)^2-8x+1\right)-1}{16x^2}=\dfrac{\left(4x\right)^2.\left(4x-1\right)^2-1}{16x^2}\)
\(=\dfrac{\left(16x^2-4x\right)^2-1}{16x^2}=\dfrac{\left(16x^2-4x-1\right)\left(16x^2-4x+1\right)}{16x^2}\)
\(=\dfrac{\left(\left(4x\right)^2-4x-1\right)\left(\left(4x\right)^2-4x+1\right)}{\left(4x\right)^2}\)