Một mảnh đất hình chữ nhật có S = 300m2 Nếu tăng chiều dài thêm 4m, giảm chiều rộng đi 1m thì diện tích mảnh đất tăng thêm 36m2
tính các kích thước của mảnh đất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi chiều dài và chiều rộng mảnh đất lần lượt là a và (m; a,b>0)
+ Mảnh đất có chu vi 70m
\(\Rightarrow2\left(a+b\right)=75\left(1\right)\)
+ Tăng chiều rộng 1m ,giảm chiều dài 5m thì diện tích mảnh đất giảm 60m2 so với ban đầu
\(\Rightarrow\left(a-5\right)\left(b+1\right)=ab-60\\ \Leftrightarrow ab+a-5b-5=ab-60\\ \Leftrightarrow a-5b=-55\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\Rightarrow hpt:\left\{{}\begin{matrix}2a+2b=70\\a-5b=-55\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=20\\b=15\end{matrix}\right.\left(TM\right)\)
Vậy chiều dài mảnh đất là 20(m) và chiều rộng mảnh đất là 15(m)
Nửa chu vi của mảnh đất là: 70:2=35(m)
Gọi chiều dài ban đầu của mảnh đất là a(m)(Điều kiện: \(0< a\le35\))
Chiều rộng ban đầu của mảnh đất là: 35-a(m)
Diện tích ban đầu của mảnh đất là: \(a\left(35-a\right)=35a-a^2\left(m^2\right)\)
Vì khi tăng chiều rộng thêm 1m và giảm chiều dài 5m thì diện tích giảm 60m2 so với ban đầu nên ta có phương trình:
\(\left(a-5\right)\left(35-a+1\right)=35a-a^2-60\)
\(\Leftrightarrow\left(a-5\right)\left(-a+36\right)=35a-a^2-60\)
\(\Leftrightarrow-a^2+36a+5a-180-35a+a^2+60=0\)
\(\Leftrightarrow6a-120=0\)
\(\Leftrightarrow6a=120\)
hay a=20(thỏa ĐK)
Chiều rộng ban đầu là: 35-20=15(m)
Vậy: Chiều dài và chiều rộng ban đầu là 20m và 15m

Gọi chiều rộng của mảnh đất là x (m, x > 0).
Diện tích bằng
240
m
2
⇒
Δ
=
3
2
–
4
.
1
.
(
-
180
)
=
729
⇒ Chiều dài mảnh đất là: 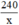 (m).
(m).
Diện tích mảnh đất sau khi tăng chiều rộng 3m, giảm chiều dài 4m là:
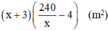
Theo bài ra: diện tích mảnh đất không đổi nên ta có phương trình:
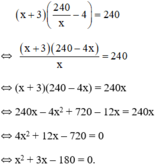
Có a = 1; b = 3; c = -180
Phương trình có hai nghiệm:
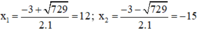
Trong hai nghiệm chỉ có nghiệm x = 12 thỏa mãn điều kiện.
Vậy mảnh đất có chiều rộng bằng 12m, chiều dài bằng 240 : 12 = 20 (m).

Gọi chiều rộng của mảnh đất là x (m, x > 0).
Diện tích bằng 240 m2 ⇒ Chiều dài mảnh đất là: 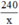 (m).
(m).
Diện tích mảnh đất sau khi tăng chiều rộng 3m, giảm chiều dài 4m là:
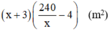
Theo bài ra: diện tích mảnh đất không đổi nên ta có phương trình:
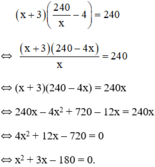
Có a = 1; b = 3; c = -180 ⇒ Δ = 32 – 4.1.(-180) = 729
Phương trình có hai nghiệm:
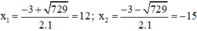
Trong hai nghiệm chỉ có nghiệm x = 12 thỏa mãn điều kiện.
Vậy mảnh đất có chiều rộng bằng 12m, chiều dài bằng 240 : 12 = 20 (m).

Gọi chiều dài, chiều rộng lần lượt là a,b
Theo đề, ta có: ab=280 và (a+10)(b-3)=ab+220
=>-3a+10b=250 và ab=280
=>-3a=250-10b và ab=280
=>a=10/3b-250/3 và b(10/3b-250/3)=280
=>b=28
=>a=10

Gọi chiều dài của mảnh đất hình chữ nhật là x (m, x > 4)
Khi đó chiều rộng của mảnh đất hình chữ nhật là \(\frac{240}{x}\left(m\right)\)
Khi tăng chiều rộng 3m, giảm chiều dài 4m thì diện tích mảnh đất là:
\(\left(x-4\right)\left(\frac{240}{x}+3\right)\)
Do diện tích không đổi nên ta có phương trình:
\(\left(x-4\right)\left(\frac{240}{x}+3\right)=240\)
\(\Rightarrow240+3x-\frac{960}{x}-12=240\)
\(\Rightarrow3x^2-12x-960=0\Rightarrow\orbr{\begin{cases}x=20\left(n\right)\\x=-16\left(l\right)\end{cases}}\)
Vậy chiều dài mảnh đất là 20m, chiều rộng mảnh đất là 12m.

Nửa chu vi mảnh đất: 21m
Gọi chiều dài mảnh đất là x (với \(10,5< x< 21\))
Chiều rộng mảnh đất là: \(21-x\) (m)
Chiếu dài mảnh đất sau khi giảm 1m: \(x-1\)
Chiều rộng mảnh đất sau khi tăng 2m: \(21-x+2=23-x\)
Diện tích mảnh đất sau khi thay đổi kích thước:
\(\left(x-1\right)\left(23-x\right)\)
Ta có pt:
\(\left(x-1\right)\left(23-x\right)=121\)
\(\Leftrightarrow-x^2+24x-144=0\Rightarrow x=12\left(m\right)\)
Vậy mảnh đất ban đầu dài 12m, rộng 9m

Phần đất tăng thêm là một hình chữ nhật có chiều rộng 4m. Chiều dài của phần đất tăng thêm là:
160 : 4 = 40 (m)
Hai lần chiều rộng mảnh đất ban đầu là:
40 + 4 = 44 (m)
Chiều rộng mảnh đất ban đầu là:
44 : 2 = 22 (m)
Chiều dài mảnh đất ban đầu là:
22 x 3 = 66 (m)
Diện tích hình chữ nhật là:
22 x 66 = 1452 ( m 2 )
Đáp số: 1452 m 2

Gọi chiều dài của hình chữ nhật ban đầu là x , m , x>15 \(x\in R\)
=> Chiều rộng của hình chữ nhật ban đầu là x-15 , m
=> Diện tích của hình chữ nhật ban đầu là \(x\left(x-15\right)\) , m2
Theo bài ra ta có :
Chiều dài của hình chữ nhật mới là : x + 5 , m
Chiều rộng của hình chữ nhật mới là : x - 5 , m
=> Diện tích hình chữ nhật mới là : \(\left(x+5\right)\left(x-5\right)\) , m2
Theo giả thiết đề nên ta có phương trình :
\(\left(x+5\right)\left(x-5\right)-x\left(x-15\right)=650\)
<=> x = 35,25 m
vậy chiều dài ban đầu là 35,25 m
chiều ring ban đầu là 20,25 m
Gọi x là chiều rộng mảnh đất. (x >0)
y là chiều dài mảnh đất. (y>0)
Ta có hệ PT xy = 300
(x-1) (y+4) = 336.
Bạn tự gải hẹ Pt đó đi rồi tìm kết quả.
Pt này khó giải quá bạn ơi