vẽ đồ thị hàm số y=2x
Hỏi điểm M(2;-40 bà N(1/2;1) có thuộc đồ thị hàm số không
vẽ và giải chi tiết
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Điểm N thuộc đồ thị vì \(y_N=1=2\cdot x_N=2\cdot\dfrac{1}{2}\)
Điểm M ko thuộc đồ thị vì \(y_M=-4< >2\cdot x_M\)
Lời giải:
ĐTHS $y=2x$:
Muốn kiểm tra xem 1 điểm có thuộc đths không thì ta thay tung độ và hoành độ của đồ thị đó vào phương trình đồ thị đó xem có thỏa mãn không là được.
$x_M=1; y_M=-4$ nên $y_M\neq 2x_M$ nên $M$ không thuộc đths $y=2x$
$x_N=\frac{1}{2}; y_N=2$ nên $y_N=2x_N$ nên $N$ thuộc đths $y=2x$

b: Để hai đường cắt nhau trên trục tung thì
m<>2 và m+1=2
=>m=1
a: 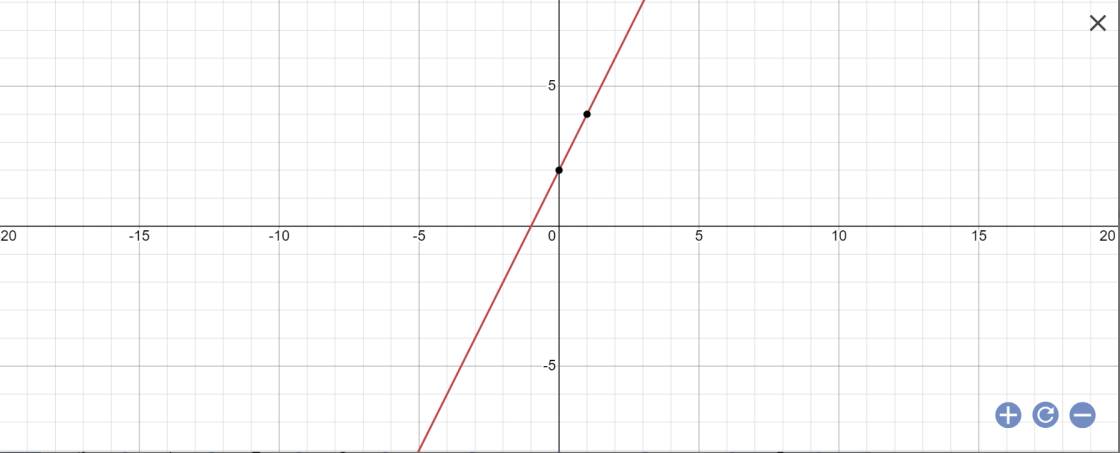

1. Đồ thị của hàm số đi qua điểm \(M\left(2;3\right)\) nên giá trị hoành độ và tung độ của \(M\) là nghiệm của phương trình đường thẳng trên, tức:
\(3=m\cdot2+m-6\Leftrightarrow m=3\left(TM\right)\)
2. Đồ thị hàm số song song với đường thẳng \(\left(d\right):y=3x+2\), khi: \(\left\{{}\begin{matrix}m=3\\m-6\ne2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m\ne8\end{matrix}\right.\Rightarrow m=3\left(TM\right)\)
3. Gọi \(P\left(x_0;y_0\right)\) là điểm cố định mà đồ thị hàm số đi qua với mọi giá trị \(m\).
Khi đó: \(mx_0+m-6=y_0\Leftrightarrow\left(x_0+1\right)m-\left(y_0+6\right)=0\left(I\right)\)
Suy ra, phương trình \(\left(I\right)\) có vô số nghiệm, điều này xảy ra khi: \(\left\{{}\begin{matrix}x_0+1=0\\y_0+6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-1\\y_0=-6\end{matrix}\right.\).
Vậy: Điểm cố định mà đồ thị hàm số luôn đi qua với mọi giá trị \(m\) là \(P\left(-1;-6\right)\).

a: Thay x=2 và y=-1 vào y=ax, ta được:
2a=-1
hay a=-1/2
M(2;-4) ạ em nhầm