 giải bài này hộ mình cái
giải bài này hộ mình cái
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1. Jim asked his girlfriend how many pairs of shoes does she have.
2. Peter asked Jane if she is going to London next week.
3. Mom asked my sister if she had done the laundry.
4. Jane asked Peter if his brother lived in London.
5. Jim asked his sister what was she doing now.
6. My classmate asked me if I enjoyed the party last night.
7. My friends always ask me what genre of music do I most.
8. My doctor asked me what had I done to cope with my work stress.
9. Jim asked me what did I often do if I was sad.
10. Jim asked me who did I run into yesterday.

1) Ta có: \(\dfrac{1}{\sqrt{3}-1}+\dfrac{1}{4+2\sqrt{3}}-\dfrac{2}{\sqrt{3}}-\dfrac{3}{2}\)
\(=\dfrac{\sqrt{3}+1}{2}+\dfrac{2-\sqrt{3}}{2}-\dfrac{2\sqrt{3}}{3}-\dfrac{3}{2}\)
\(=\dfrac{\sqrt{3}+1+2-\sqrt{3}-3}{2}-\dfrac{2\sqrt{3}}{3}\)
\(=-\dfrac{2\sqrt{3}}{3}\)
3) Ta có: \(\dfrac{\sqrt{10}+\sqrt{15}}{\sqrt{8}+\sqrt{12}}-\dfrac{3\sqrt{5}}{4}\)
\(=\dfrac{\sqrt{5}\left(\sqrt{2}+\sqrt{3}\right)}{2\left(\sqrt{2}+\sqrt{3}\right)}-\dfrac{3\sqrt{5}}{4}\)
\(=\dfrac{2\sqrt{5}-3\sqrt{5}}{4}\)
\(=\dfrac{-\sqrt{5}}{4}\)

\(2x+\frac{\pi}{6}=\frac{\pi}{2}+k\pi\)
\(\Leftrightarrow2x=\frac{\pi}{3}+k\pi\)
\(\Leftrightarrow x=\frac{\pi}{6}+\frac{k\pi}{2}\)

Bài 5 hình 1: (tự vẽ hình nhé bạn)
a) Xét ΔABD và ΔACB ta có:
\(\widehat{BAD}\)= \(\widehat{BAC}\) (góc chung)
\(\widehat{ABD}\)= \(\widehat{ACB}\) (gt)
=> ΔABD ~ ΔACB (g-g)
=> \(\dfrac{AB}{AC}\) = \(\dfrac{BD}{CB}\) = \(\dfrac{AD}{AB}\) (tsđd)
b) Ta có: \(\dfrac{AB}{AC}\) = \(\dfrac{AD}{AB}\) (cm a)
=> \(AB^2\) = AD.AC
=> \(2^2\) = AD.4
=> AD = 1 (cm)
Ta có: AC = AD + DC (D thuộc AC)
=> 4 = 1 + DC
=> DC = 3 (cm)
c) Xét ΔABH và ΔADE ta có:
\(\widehat{AHB}\) = \(\widehat{AED}\) (=\(90^0\))
\(\widehat{ADB}\) = \(\widehat{ABH}\) (ΔABD ~ ΔACB)
=> ΔABH ~ ΔADE
=> \(\dfrac{AB}{AD}\) = \(\dfrac{AH}{AE}\) = \(\dfrac{BH}{DE}\) (tsdd)
Ta có: \(\dfrac{S_{ABH}}{S_{ADE}}\) = \(\left(\dfrac{AB}{AD}\right)^2\)= \(\left(\dfrac{2}{1}\right)^2\)= 4
=> đpcm
Tiếp bài 5 hình 2 (tự vẽ hình)
a) Xét ΔABC vuông tại A ta có:
\(BC^2\) = \(AB^2\) + \(AC^2\)
\(BC^2\) = \(21^2\) + \(28^2\)
BC = 35 (cm)
b) Xét ΔABC và ΔHBA ta có:
\(\widehat{BAC}\) = \(\widehat{AHB}\) ( =\(90^0\))
\(\widehat{ABC}\) = \(\widehat{ABH}\) (góc chung)
=> ΔABC ~ ΔHBA (g-g)
=> \(\dfrac{AB}{BH}\) = \(\dfrac{BC}{AB}\) (tsdd)
=> \(AB^2\) = BH.BC
=> \(21^2\) = 35.BH
=> BH = 12,6 (cm)
c) Xét ΔABC ta có:
BD là đường p/g (gt)
=> \(\dfrac{AD}{DC}\) = \(\dfrac{AB}{BC}\) (t/c đường p/g)
Xét ΔABH ta có:
BE là đường p/g (gt)
=> \(\dfrac{HE}{AE}\) = \(\dfrac{BH}{AB}\) (t/c đường p/g)
Mà: \(\dfrac{AB}{BC}\) = \(\dfrac{BH}{AB}\) (cm b)
=> đpcm
d) Ta có: \(\left\{{}\begin{matrix}\widehat{HBE}+\widehat{BEH}=90^0\\\widehat{ABD}+\widehat{ADB=90^0}\\\widehat{HBE}=\widehat{ABD}\end{matrix}\right.\)
=> \(\widehat{BEH}=\widehat{ADB}\)
Mà \(\widehat{BEH}=\widehat{AED}\) (2 góc dd)
Nên \(\widehat{ADB}=\widehat{AED}\)
=> đpcm

suy ra 1 trong 2 so la so am
ma (x^2-8) lon hon (x^2-39) nen (x^2 -39) la am
xong thi tu lap luan
\(\left(x^2-8\right)\left(x^2-39\right)< 0\)
TH1 : Cả 2 cùng âm
\(\hept{\begin{cases}x^2-8< 0\\x^2-39< 0\end{cases}=>\hept{\begin{cases}x< 2,828.....\\x< 6,244........\end{cases}}}\)
TH2 : Cả 2 cùng dương
\(\hept{\begin{cases}x^2-8>0\\x^2-39>0\end{cases}=>\hept{\begin{cases}x>2,82.......\\x>6,244......\end{cases}}}\)



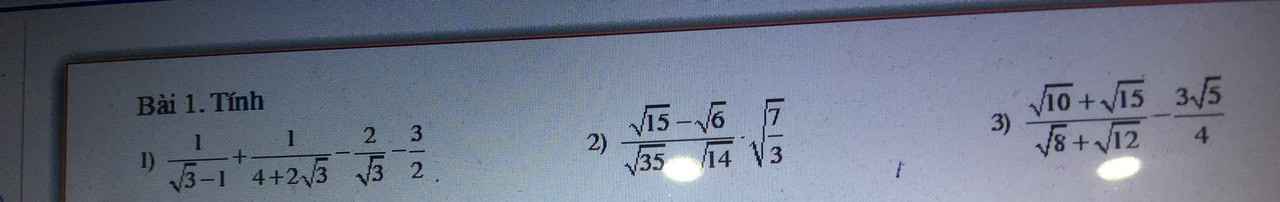
 Ai giải chi tiết cái này hộ mình với
Ai giải chi tiết cái này hộ mình với giải hộ mình mấy bài này vs ạ !
giải hộ mình mấy bài này vs ạ !


Thùng thứ nhất chứa số lít là:
\(33,8+17,5=51,3\left(l\right)\)
Cả hai thùng chứa số lít là:
\(51,3+33,8=85,1\left(l\right)\)