Cho hàm số y = f(x) = 2x2 – 1 ; Tính f(- 1); f( -2) ; f(1) f(2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)\(f\left(1\right)=2.1^2+5.1-3=2+5-3=4\)
\(f\left(0\right)=0+0-3=-3\)
\(f\left(1,5\right)=2.\left(1,5\right)^2-5.1,5-3=4,5-7,5-3=-6\)

Đáp án A
![]()
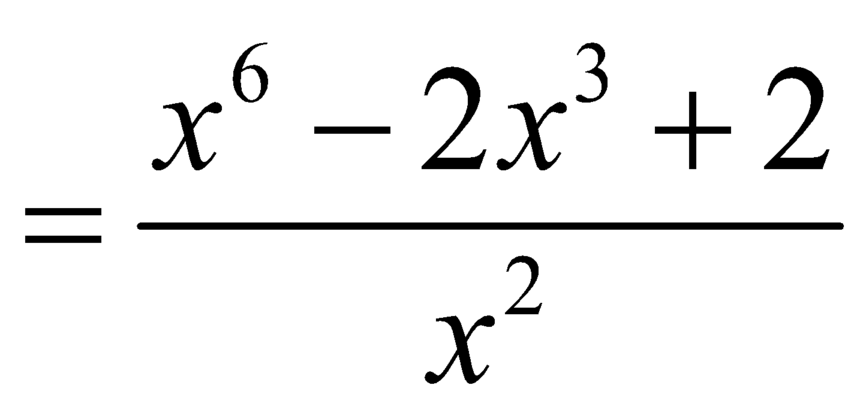
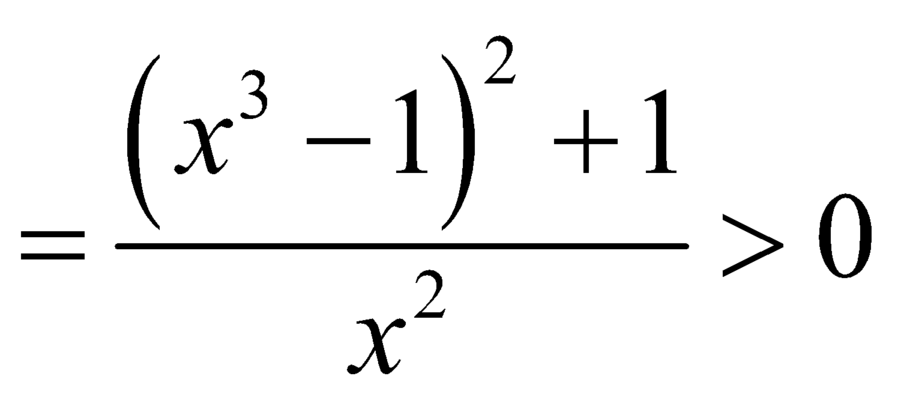 ,
, ![]() .
.
![]() đồng biến trên
đồng biến trên ![]() .
.
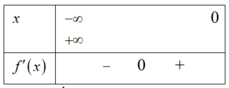
![]() có nhiều nhất
có nhiều nhất ![]() nghiệm trên khoảng
nghiệm trên khoảng ![]()
![]() .
.
Mặt khác ta có:
![]() ,
, ![]()
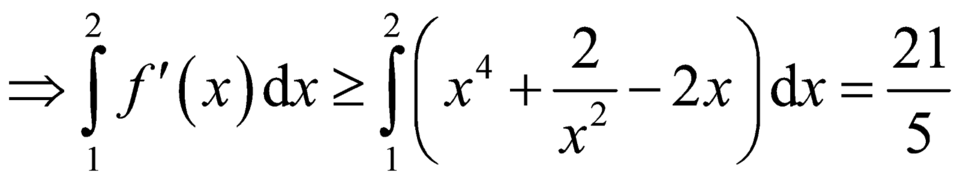
khoảng (1;2)
![]()
![]() .
.
Kết hợp giả thiết ta có ![]() liên tục trên
liên tục trên ![]() và
và ![]()
![]() .
.
Từ (1) và (2) suy ra phương trình f(x) = 0 có đúng 1 nghiệm trên khoảng (1;2)

`a)`
`@f(1)=2.1^2+5.1-3=2.1+5-3=2+5-3=4`
`@f(0)=2.0^2+5.0-3=-3`
`@f(1,5)=2.(1,5)^2+5.1,5-3=4,5+7,5-3=9`
_____________________________________________________
`b)`
`***f(3)=9`
`=>3a-3=9`
`=>3a=12=>a=4`
`***f(5)=11`
`=>5a-3=11`
`=>5a=14=>a=14/5`
`***f(-1)=6`
`=>-a-3=6`
`=>-a=9=>a=-9`
a: f(1)=2+5-3=4
f(0)=-3
f(1,5)=4,5+7,5-3=9
b: f(3)=9 nên 3a-3=9
hay a=4
f(5)=11 nên 5a-3=11
hay a=14/5
f(-1)=6 nên -a-3=6
=>-a=9
hay a=-9

Bài 1:
\(f\left(-1\right)=1\)
\(f\left(\dfrac{1}{2}\right)=-\dfrac{1}{2}\)
\(f\left(0\right)=-1\)
\(f\left(-5\right)=49\)
Bài 2:
Bạn lấy toạ độ điểm A(1;3); B(-1;-3), C(0;0). Đồ thị y=3x một đường thẳng đi qua gốc toạ độ O nhé!

Ta có: f(1) = 2.12 – 5 = 2 – 5 = -3
f(-2) = 2.(-2)2 – 5 = 8 – 5 = 3
f(0) = 2.02 – 5 = 0 – 5 = -5
f(2) = 2.22 – 5 = 2.4 – 5 = 3

\(g\left(x\right)=f\left(1-2018x\right)\Rightarrow g'\left(x\right)=-2018f'\left(1-2018x\right)\)
\(\Rightarrow\) Số nghiệm của \(g'\left(x\right)\) bằng số nghiệm \(f'\left(x\right)\Rightarrow g'\left(x\right)\) có 4 nghiệm
\(g\left(x\right)=0\Leftrightarrow f\left(1-2018x\right)=0\) có số nghiệm bằng số nghiệm f(x)
Do \(f'\left(x\right)\) có 4 nghiệm nên f(x) có tối đa 5 nghiệm
Vậy hàm có tối đa 9 cực trị

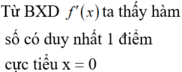
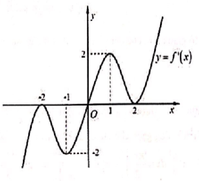
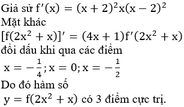

\(y=f\left(x\right)=2x^2-1.\)
\(f\left(-1\right)=2.\left(-1\right)^2-1=1.\)
\(f\left(-2\right)=2.\left(-2\right)^2-1=7.\)
\(f\left(1\right)=2.1^2-1=1.\)
\(f\left(2\right)=2.2^2-1=7.\)