Cho đa thức g(x) thỏa mãn: (x-1)g(-x) + g(x) = x+2 đúng với mọi giá trị x. Tính g(-2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TH
1
8 tháng 4 2016
thayx=-2 ta có(-3)g(2)+g(-2)=0 (1)
thay x=2 ta có g(-2)+g(2)=4
->3g(-2)+3g(2)=12 (2)
lấy từng vế của (1)+(2) ta có
4g(-2)=12
->g(-2)=3
Vậy g(-2)=3
PQ
0
12 tháng 4 2022
a: \(f\left(-2\right)=5\cdot4-8-8=4\)
b: \(f\left(x\right)+g\left(x\right)=6x^2+2x-8\)
c: Đặt G(x)=0
=>x(x-2)=0
=>x=0 hoặc x=2
AD
23 tháng 7 2021
a) \(f\left(x\right)-g\left(x\right)=\left[x\left(x^2-2x+7\right)-1\right]-\left[x\left(x^2-2x-1\right)-1\right]\)
\(f\left(x\right)-g\left(x\right)=x^3-2x^2+7x-1-x^3+2x^2+x+1\)
\(f\left(x\right)-g\left(x\right)=8x\)
\(f\left(x\right)+g\left(x\right)=x\left(x^2-2x+7\right)-1+x\left(x^2-2x-1\right)-1\)
\(f\left(x\right)+g\left(x\right)=x^3-2x^2+7x-1+x^3-2x^2-x-1\)
\(f\left(x\right)+g\left(x\right)=2x^3-4x^2+6x-2\)
b) 8x=0
=> x=0
=> Nghiệm đa thức f(x)-g(x)
c) Thay \(x=-\frac{3}{2}\)vào BT f(x)+g(x) ta được :
\(2.\left(-\frac{3}{2}\right)^3-4\left(-\frac{3}{2}\right)^2+6\left(-\frac{3}{2}\right)-2\)
\(=6,75+9-9-2\)
\(=4,75\)
#H
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
G(-2) = (-2)2 – 4 = 4 – 4 = 0;
G(1) = 12 – 4 = 1 – 4 = -3;
G(0) = 02 – 4 = 0 – 4 = -4;
G(1) = 12 – 4 = 1- 4 = -3;
G(2) = 22 – 4 = 4 – 4 = 0
9 tháng 11 2023
1:
\(f\left(x\right)=g\left(x\right)\cdot p\left(x\right)\)
=>\(p\left(x\right)=\dfrac{f\left(x\right)}{g\left(x\right)}\)
\(=\dfrac{x^5-3x^4+7x^3-9x^2+8x-2}{x^2-2x+a}\)
Để P(x) tồn tại với mọi x thì \(x^2-2x+a< >0\)(2) với mọi x
Giả sử \(x^2-2x+a=0\)(1)
\(\text{Δ}=\left(-2\right)^2-4\cdot1\cdot a=4-4a\)
Để phương trình (1)có nghiệm thì 4-4a>=0
=>a<=1
Do đó: Để bất phương trình (2) luôn đúng với mọi x thì a>1
Bài 3:
1:
AH=AO
=>H trùng với O
=>Tâm đường tròn ngoại tiếp ΔABC trùng với trực tâm của tam giác
=>ΔABC đều
=>\(\widehat{BAC}=60^0\)
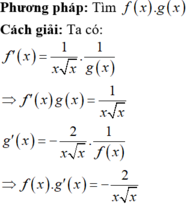
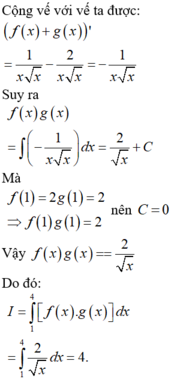
Ai giải hộ giúp
g(-2) = 3