Nguyên tử Mg có ba đồng vị ứng với thành phần phần trăm về số nguyên tử như sau :
Đồng vị 24Mg 25Mg 26Mg
% 78,6 10,1 11,3
a. Tính nguyên tử khối trung bình của Mg.
b. Giả sử trong hỗn hợp nói trên có 50 nguyên tử 25Mg , thì số nguyên tử tương ứng của hai đồng vị còn lại là bao nhiêu ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đặt %24Mg là x
-->%25Mg là (100 - x - 11)
\(\overline{M}=\dfrac{x.24+\left(100-x-11\right).25+11.26}{100}=24,32\)
\(\Rightarrow x=\%^{24}Mg=79\%\)
b) ta có : \(n_{Mg}=n_{MgCl2}=1\left(mol\right)\Rightarrow n_{26_{Mg}}=1.11\%=0,11\left(mol\right)\)
Số nguyên tử : \(0,11.6,022.10^{-3}=6,6022.10^{-4}\)(nguyên tử)

Đáp án B.
Do electron có khối lượng rất nhỏ nên nguyên tử khối trung bình của Mg xấp xỉ bằng số khối trung bình của nó:
![]()

Đáp án C.
Ta có:
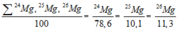
Giả sử trong hỗn hợp nói trên có 50 nguyên tử 25Mg, thì số nguyên tử tương ứng của 2 đồng vị còn lại là:
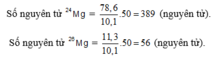

Đáp án C
Nguyên tử khối trung bình của Mg là
MMg = ( 24 . 78 , 99 + 25 . 10 + 26 . 11 , 01 ) / 100 = 24 , 3202

Gọi lần lượt số nguyên tử đồng vị 25Mg và 24Mg trong 500 nguyên tử là a,b (a,b >0)
Ta có : a + b = 500 (1)
Vì nguyên tử khối trung bình của nguyên tử Mg là 24,4 nên :
25a + 24b = 24,4.500 (2)
Từ (1) và (2) => \(\left\{{}\begin{matrix}a=200\\b=300\end{matrix}\right.\)
Vậy ...

\(A=78,99\%.24+10\%.25+11,01\%.26=24,32\)
\(\Rightarrow\%25Mg=10\%\)nên nếu có 50 ng tử 25Mg thì tổng số ng tử : \(\frac{50}{10\%}=500\)
Số ng tử 24Mg = \(500.78,99\%=394,95\)
Số ng tử 26Mg = \(500.11,01\%=55,05\)

Phần trăm đồng vị thứ nhất \(^{24}Mg\) là 78,6%.
Gọi phần trăm đồng vị \(^{25}Mg\) và \(^{26}Mg\) lần lượt là a và b.
\(\Rightarrow\left\{{}\begin{matrix}78,6\%+a\%+b\%=100\%\\24\cdot78,6\%+25\cdot a\%+26\cdot b\%=24,327\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=10,1\%\\b=11,3\%\end{matrix}\right.\)


a, Ta có : \(A=78,6\)%\(.24+10,1\)%.\(25+11,3\)%.\(26=24,327\)
b, \(24Mg\) 25Mg 26Mg
78,6% 10,1% 11,3%
\(x\) <--- 25 nguyên tử <-- \(y\)
Nhân chéo : \(x=\dfrac{25.78,6}{10} = 196,5 \) nguyên tử
\(y=\dfrac{25.11,3}{10} ≈28 \) nguyên tử
Đề là 50 nguyên tử ko phải 25 nguyên tử đâu ạ.