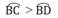cho tam giác ABC nội tiếp đường tròn tâm O. Biết A=50 độ, B=65 độ. Kẻ OH vuông AB, OI vuông AC, OK vuông BC. So sánh OH, OK, OI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
M
Minz
7 tháng 1 2022
Đúng(1)
Những câu hỏi liên quan
CM
23 tháng 3 2019
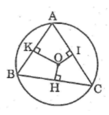
Tam giác ABC có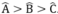 
nên suy ra :
BC > AC > AB (cạnh đối diện góc lớn hơn thì lớn hơn)
Ta có AB, BC, AC lần lượt là các dây cung của đường tròn (O)
Mà BC > AC > AB nên suy ra:
OH < OI < OK (dây lớn hơn gần tâm hơn)
3 tháng 12 2023
Xét ΔABC có \(\widehat{BAC}>\widehat{ABC}>\widehat{ACB}\)
mà BC là cạnh đối diện của góc BAC
và AC là cạnh đối diện của góc ABC
và AB là cạnh đối diện của góc ACB
nên BC>AC>AB
Xét (O) có
BC,AC,AB là các dây
BC>AC>AB
OH,OI,OK lần lượt là khoảng cách từ tâm O đến các dây BC,AC,AB
Do đó: OH<OI<OK
24 tháng 6 2017
Ta có \(\widehat{A}>\widehat{B}>\widehat{C}\) nên \(BC>AC>AB\)
Do đó \(OH< OI< OK\)
23 tháng 8 2019
Tam giác ABC có ˆA>ˆB>ˆCA^>B^>C^ nên suy ra:
BC > AC > AB (cạnh đối diện góc lớn hơn thì lớn hơn)
Ta có AB, BC, AC lần lượt là các dây cung của đường tròn (O)
Mà BC < AC > AB nên suy ra:
OH < OI < OK ( dây lớn hơn gần tâm hơn).
Chúc bạn học tốt !!!
CM
8 tháng 7 2018
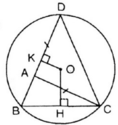
a) Xét ΔABC có: BC < AB + AC (Bất đẳng thức tam giác)
Mà AD = AC (gt)
⇒ BC < AB + AD = BD
Mà OH là khoảng cách từ O đến dây BC
OK là khoảng cách từ O đến dây BD
⇒ OH > OK.( định lý về khoảng cách từ tâm đến dây)
b) Vì BD > BC
⇒ 
Kiến thức áp dụng
+ Trong một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn
+ Trong một đường tròn, dây lớn hơn căng cung lớn hơn.
CM
29 tháng 8 2017
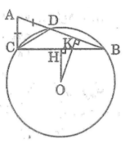
Theo câu a ,BC > BD
Vì trong một đường tròn, dây cung lớn hơn căng cung lớn hơn nên :
