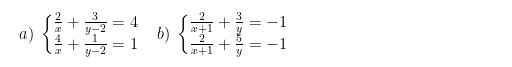
Giúp mình với ạ
Mình cảm ơn nhiều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a have
b to wear
c do
d couldn't
e to live
f to do
g stay
h since
i for
j did

CÂU 1:
\(\dfrac{6x^2y^2}{8xy^5}=\dfrac{3x}{4y^3}\)
CÂU 2:
\(\dfrac{12x^3y^2}{18xy^5}=\dfrac{2x^2}{3y^3}\)
CÂU 3:
\(\dfrac{15x\left(x+5\right)^3}{20x^2\left(x+5\right)}=\dfrac{3\left(x+5\right)^2}{4x}\)
CÂU 4:
\(\dfrac{3xy+x}{9y+3}=\dfrac{x\left(3y+1\right)}{3\left(3y+1\right)}=\dfrac{x}{3}\)
CÂU 5:
\(\dfrac{3xy+3x}{9y+9}=\dfrac{3x\left(y+1\right)}{9\left(y+1\right)}=\dfrac{x}{3}\)
CÂU 6:
\(\dfrac{x^2-xy}{5y^2-5xy}=\dfrac{x\left(x-y\right)}{5y\left(y-x\right)}=\dfrac{-x\left(y-x\right)}{5y\left(y-x\right)}=\dfrac{-x}{5y}\)
CÂU 7:
\(\dfrac{2x^2+2x}{x+1}=\dfrac{2x\left(x+1\right)}{x+1}=2x\)
CÂU 8:
\(\dfrac{7x^2+14x+7}{3x^2+3x}=\dfrac{7\left(x^2+2x+1\right)}{3x\left(x+1\right)}\\ =\dfrac{7\left(x+1\right)^2}{3x\left(x+1\right)}=\dfrac{7\left(x+1\right)}{3x}\)
CÂU 9:
\(\dfrac{10xy^2\left(x+y\right)}{15xy\left(x+y\right)^3}=\dfrac{2y}{3\left(x+y\right)^2}\)


a: BC=căn 6^2+8^2=10cm
bD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=8/8=1
=>AD=3cm; CD=5cm
b: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
góc B chung
=>ΔBHA đồng dạng với ΔBAC
=>BH/BA=BA/BC
=>BH*BC=BA^2
c: Xét ΔBHA có BI là phân giác
nên IH/IA=BH/BA
=>IH/IA=BA/BC=AD/DC

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{2a-3b}{2\cdot5-3\cdot2}=\dfrac{12}{4}=3\)
Do đó: a=15; b=6
d) Áp dụng t/c dtsbn:
\(\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{2a}{10}=\dfrac{3b}{6}=\dfrac{2a-3b}{10-6}=\dfrac{12}{4}=3\)
\(\Rightarrow\left\{{}\begin{matrix}a=3.5=15\\b=3.2=6\end{matrix}\right.\)
f) \(\Rightarrow\dfrac{x}{5}=\dfrac{y}{3}=-\dfrac{z}{2}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{-z}{2}=\dfrac{x+y-z}{5+3+2}=\dfrac{2}{10}=\dfrac{1}{5}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{5}.5=1\\y=\dfrac{1}{5}.3=\dfrac{3}{5}\\z=\dfrac{1}{5}.\left(-2\right)=-\dfrac{2}{5}\end{matrix}\right.\)
g) \(\dfrac{x}{4}=\dfrac{y}{5}=k\)\(\Rightarrow\left\{{}\begin{matrix}x=4k\\y=5k\end{matrix}\right.\)
\(\Rightarrow xy=20k^2=500\Rightarrow k=\pm5\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=20\\y=25\end{matrix}\right.\\\left\{{}\begin{matrix}x=-20\\y=-25\end{matrix}\right.\end{matrix}\right.\)


mở bài là giới thiệu về cụ nha mn em viết lộn ạ
thân bài là đóng góp ạ




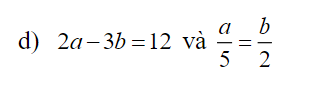
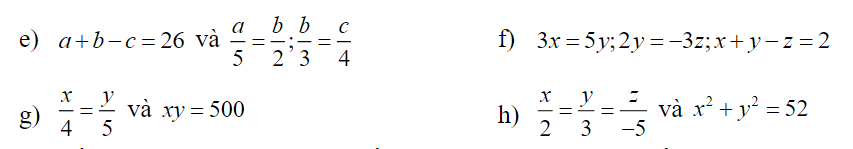


 Mọi người giúp mình với ạ! Mình cảm ơn nhiều ạ!
Mọi người giúp mình với ạ! Mình cảm ơn nhiều ạ!

a: Đặt 1/x=a
1/(y-2)=b
Hệ phương trình trở thành:
\(\left\{{}\begin{matrix}2a+3b=4\\4a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a+6b=8\\4a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5b=7\\4a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{7}{5}\\a=-\dfrac{1}{10}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{-1}{10}\\\dfrac{1}{y-2}=\dfrac{7}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-10\\y-2=\dfrac{5}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-10\\y=\dfrac{19}{7}\end{matrix}\right.\)
b: \(\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{2}{y}=0\\\dfrac{2}{x+1}+\dfrac{3}{y}=-1\end{matrix}\right.\)
=>Hệ phương trình vô nghiệm
a) \(\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{3}{y-2}=4.\\\dfrac{4}{x}+\dfrac{1}{y-2}=1.\end{matrix}\right.\) \(ĐK:x\ne0;y\ne2.\)
Đặt \(\dfrac{1}{x}=a;\dfrac{1}{y-2}=b\left(a;b\ne0\right).\)
\(\Rightarrow\left\{{}\begin{matrix}2a+3b=4.\\4a+b=1.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{-1}{10}.\\b=\dfrac{7}{5}.\end{matrix}\right.\) (TM).
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{-1}{10}.\\\dfrac{1}{y-2}=\dfrac{7}{5}.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-10\left(TM\right).\\y=\dfrac{19}{7}\left(TM\right).\end{matrix}\right.\)
Vậy hệ phương trình có nghiệm \(\left(x;y\right)=\left(-10;\dfrac{19}{7}\right).\)