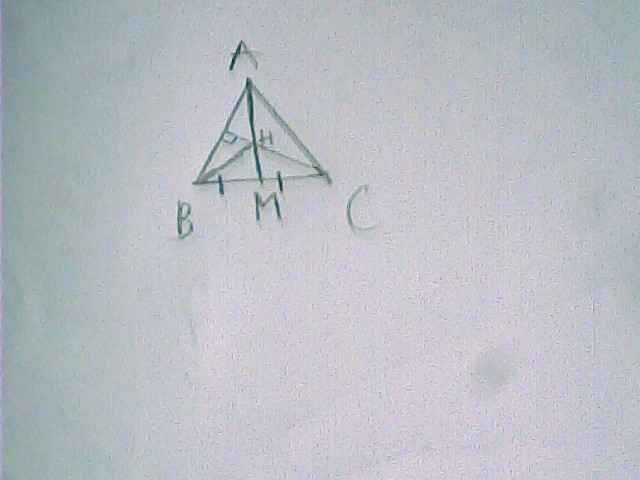
ho ABC có AB = AC. Gọi M là trung điểm của BC.
a) Chứng minh: ∆ABM = ∆ACM và AM vuông góc BC
b) Qua điểm C vẽ đường thẳng vuông góc với AC, đường thẳng này cắt tia AM tại H.
Chứng minh: ∆HBM = ∆HCM và HM là tia phân giác của BHC
c) Chứng minh: ∆ABH = ∆ACH và AB vuông góc HB
Cho mk xin hình luôn được ko ạ

a, xét tam giác abm và tam giác amc có:
am chung
bm = mc(gt)
ab=ac(gt)
=> tam giác abm = tam giác amc (c.c.c)
vì 2 tam giác chứng minh trên:
suy ra góc amb = góc amc (cặp góc tương ứng)
ta có amb + amc =180( kề bù)
mà amb = amc(cmt)
=> amb =90 độ
=> am vuông góc mb
=> am vuông góc bc
b, xét tam giác hbm và tam giác hcm có:
bm =mc(gt)
bmh=cmh( vì 2 góc cm ở trên)
hm chung
=> 2 tam giác cần cm bằng nhau
vì tam giác hbm = tam giác hcm(cmt)
=> góc bhm = góc chm( cặp góc tương ứng)
=> hm là tia p/g của góc bhc
c,vì tam giác hbm = tam giác hcm(cmt)
=> hb=hc( cặp cạnh tương ứng)
xét tam giác abh và tam giác ach có:
ab =ac(gt)
ah chung
bh=hc(cmt)
=> tam giác abh = tam giác ach
còn cái ab vuông góc hb thì mình ko nhìn đc bạn nhé
chúc bạn học tốt
hình đây bạn nhé, nếu câu c phần cuối bạn đánh sai thì báo mình để mình làm nốt