Cho ABC có AB = AC. Gọi M là trung điểm của BC.
a) Chứng minh: ∆ABM = ∆ACM và AM BC
b) Qua điểm C vẽ đường thẳng vuông góc với AC, đường thẳng này cắt tia AM tại H.
Chứng minh: ∆HBM = ∆HCM và HM là tia phân giác của BHC
c) Chứng minh: ∆ABH = ∆ACH và AB HB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 1 2022
a, xét tam giác abm và tam giác amc có:
am chung
bm = mc(gt)
ab=ac(gt)
=> tam giác abm = tam giác amc (c.c.c)
vì 2 tam giác chứng minh trên:
suy ra góc amb = góc amc (cặp góc tương ứng)
ta có amb + amc =180( kề bù)
mà amb = amc(cmt)
=> amb =90 độ
=> am vuông góc mb
=> am vuông góc bc
b, xét tam giác hbm và tam giác hcm có:
bm =mc(gt)
bmh=cmh( vì 2 góc cm ở trên)
hm chung
=> 2 tam giác cần cm bằng nhau
vì tam giác hbm = tam giác hcm(cmt)
=> góc bhm = góc chm( cặp góc tương ứng)
=> hm là tia p/g của góc bhc
c,vì tam giác hbm = tam giác hcm(cmt)
=> hb=hc( cặp cạnh tương ứng)
xét tam giác abh và tam giác ach có:
ab =ac(gt)
ah chung
bh=hc(cmt)
=> tam giác abh = tam giác ach
còn cái ab vuông góc hb thì mình ko nhìn đc bạn nhé
chúc bạn học tốt
7 tháng 1 2022
hình đây bạn nhé, nếu câu c phần cuối bạn đánh sai thì báo mình để mình làm nốt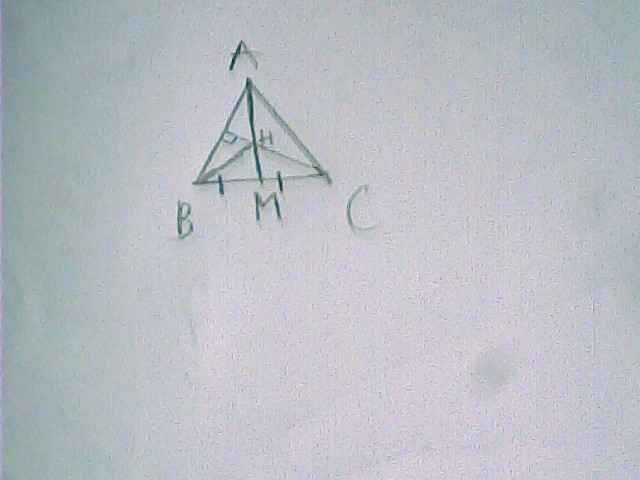
31 tháng 12 2023
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
b: Xét ΔMAB vuông tại M và ΔMDC vuông tại M có
MB=MC
\(\widehat{MBA}=\widehat{MCD}\)(hai góc so le trong, AB//CD)
Do đó: ΔMAB=ΔMDC
Ta có: \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
\(\widehat{ABC}=\widehat{DCB}\)(hai góc so le trong, AB//CD)
Do đó: \(\widehat{ACB}=\widehat{DCB}\)
=>CB là phân giác của góc ACD
8 tháng 4 2022
a: XétΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó:ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường trung trực của BC
c: Xét ΔMCE có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔMCE cân tại C
mà CA là đường cao
nên CA là tia phân giác của góc MCE
AD
3 tháng 1 2021
*Tự vẽ hình
a) Xét tam giác ABM và ACM, có :
AB=AC(GT)
AM-cạnh chung
BM=MC(GT)
-> Tam giác ABM=ACM(c.c.c)
b) Do tam giác ABM=ACM (cmt)
-> \(\widehat{AMB}=\widehat{AMC}=90^o\)
-> AM vuông góc BC
c) Xét tam giác AEI và MBI, có :
\(\widehat{EAI}=\widehat{BMI}=90^o\)
\(\widehat{AIE}=\widehat{BIM}\left(đđ\right)\)
AI=IM(GT)
-> tam giác AEI=MBI(g.c.g)
-> AE=BM ( đccm)
d) Chịu. Tự làm nhe -_-'
#Hoctot
11 tháng 1 2021
bạn tự vẽ hình
a, xét tam giác ABM và tam giác ACM có :
AB=AC (gt)
MB=MC (gt)
AM là cạch chung
suy ra tam giác ABM =tam giác ACN (c.c.c)
b, Vì tam giác ABM = tam giác ACN (câu a)
suy ra góc M1= góc M2 (2 góc tương ứng)
mà M1+M2=180 ( 2 góc kề bù)
suy ra : M1=M2= 90
suy ra AM vuông góc BC
c, Vì tam giác ABM = tam giác ACM (câu a)
suy ra : A1=A2 ( 2 góc tương ứng)
suy ra: AM là phân giác góc BAC
17 tháng 12 2021
a: Xét ΔABH và ΔACH có
AB=AC
AH chung
HB=HC
Do đó: ΔABH=ΔACH
17 tháng 12 2021
a: Xét ΔABH và ΔACH có
AB=AC
AH chung
HB=HC
Do đó: ΔAHB=ΔAHC
18 tháng 12 2021
a: Xét ΔABH và ΔACH có
AB=AC
AH chung
HB=HC
Do đó: ΔABH=ΔACH
lỗi rồi
Lỗi