2x2=bao nhiêu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có: Δ = 4 m − 1 2 − 4.2. 2 m − 1 = 4 m − 3 2
2 x 2 + 2 x 2 − 4 m − 1 x 2 + 2 x + 2 m − 1 = 0
⇔ x 2 + 2 x = 1 2 ( 1 ) x 2 + 2 x = 2 m − 1 ( 2 )
( 1 ) ⇔ x 2 + 2 x − 1 2 = 0 ⇔ x = − 2 + 6 2 ∉ − 3 ; 0 x = − 2 − 6 2 ∈ − 3 ; 0
Do đó (1) chỉ có 1 nghiệm thuộc − 3 ; 0
Để phương trình đã cho có 3 nghiệm thuộc đoạn − 3 ; 0 thì phương trình (2) phải có hai nghiệm phân biệt thuộc đoạn và hai nghiệm này phải khác − 2 − 6 2
2 ⇔ x + 1 2 = 2 m
Phương trình (2) có hai nghiệm phân biệt khác − 2 − 6 2 và thuộc đoạn − 3 ; 0
⇔ 2 m > 0 − 2 − 6 2 + 1 2 ≠ 2 m − 3 ≤ − 1 + 2 m ≤ 0 − 3 ≤ − 1 − 2 m ≤ 0 ⇔ m > 0 m ≠ 3 4 m ≤ 1 2 m ≤ 2
Không có giá trị nào của m thỏa mãn.
Đáp án cần chọn là: D

Ta có: Δ = 4 m − 3 2 − 4.2. 1 − 2 m = 4 m − 1 2
2 x 2 + 2 x 2 − 4 m − 3 x 2 + 2 x + 1 − 2 m = 0 ⇔ x 2 + 2 x = 1 2 ( 1 ) x 2 + 2 x = 2 m − 1 ( 2 )
( 1 ) ⇔ x 2 + 2 x − 1 2 = 0 ⇔ x = − 2 + 6 2 ∉ − 3 ; 0 x = − 2 − 6 2 ∈ − 3 ; 0
2 ⇔ x + 1 2 = 2 m . Phương trình đã cho có đúng 1 nghiệm thuộc đoạn - 3 ; 0 khi và chỉ khi phương trình (2) có nghiệm nhưng không thuộc đoạn - 3 ; 0 hoặc vô nghiệm.
Xét (2), nếu m < 0 thì (2) vô nghiệm (thỏa mãn yêu cầu).
+) Nếu m = 0 thì (2) có nghiệm duy nhất x = - 1 ∈ - 3 ; 0 (không thỏa yêu cầu).
+) Nếu m > 0 thì (2) có hai nghiệm phân biệt x 1 = − 1 − 2 m < − 1 + 2 m = x 2 nên (2) có hai nghiệm không thuộc - 3 ; 0 nếu
− 1 − 2 m < − 3 − 1 + 2 m > 0 ⇔ m > 2 m > 1 2 ⇔ m > 2
Vậy m < 0 m > 2
Mà m ∈ - 2019 ; 2019 và m ∈ Z nên m ∈ - 2018 ; - 2017 ; . . . ; - 1 ; 3 ; 4 ; . . . ; 2018
Số các giá trị của m thỏa mãn bài toán là 2018 + 2016 = 4034.
Đáp án cần chọn là: D

Đáp án B
Phương pháp: ax = b ⇔ x = logab (0 < a ≠ 1; b > 0)
Cách giải:
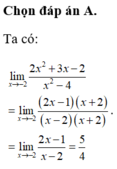
2x2=4
ai k mình mình k lại,kết bạn luôn để biết
tích trên có kết quả là :
2 x 2 = 22 = 2 ^ 2 = 4
đáp số : 4