chứng minh: Điểm cách đều 3 đỉnh của một tam giac vuông là trung điểm của cạnh huyền của tam giác đó.
Từ đó hãy tính độ dài đường trung tuyến xuất phát từ đỉnh góc vuông theo độ dài cạnh huyền của một tam giác vuông.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 5 2017
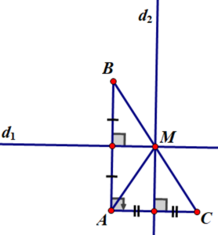
+ Giả sử ∆ABC vuông tại A.
d1 là đường trung trực cạnh AB, d2 là đường trung trực cạnh AC.
d1 cắt d2 tại M. Khi đó M là điểm cách đều ba đỉnh của tam giác ABC.
+ Áp dụng kết quả bài 55 ta có B, M, C thẳng hàng.
QUẢNG CÁO+ M cách đều A, B, C ⇒ MB = MC ⇒ M là trung điểm của cạnh BC (đpcm)
+ M là trung điểm của cạnh BC (đpcm)
*) Giả sử AM là trung tuyến của tam giác ABC suy ra M là trung điểm của cạnh BC
⇒ MB = MC = BC/2
Mà MA = MB = MC (cmt)
⇒ MA = BC/2
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.
19 tháng 4 2017
a) Giả sử ∆ABC vuông góc tại A. Vẽ hai đường trung trực của hai cạnh góc vuông AB, AC cắt nhau tại M. Ta chứng minh M là trung điểm của BC.
Vì M là giao điểm hai đường trung trực d1, d2
của AB, AC mà AB ⊥ AC nên B, M, C thẳng hàng (bài tập 55)
Vì MA = MB (M thuộc đường trung trực của AB)
MA = MC (M thuộc đường trung trực của AC)
=> MB = MC
Do B, M, C thẳng hàng và M cách đều BC nên M là trung điểm của BC
b) M là trung điểm Bc => MB = 1212 BC
mà AM = MB nên MA =1212 BC
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.
19 tháng 4 2017
a) Giả sử ∆ABC vuông góc tại A. Vẽ hai đường trung trực của hai cạnh góc vuông AB, AC cắt nhau tại M. Ta chứng minh M là trung điểm của BC.
Vì M là giao điểm hai đường trung trực d1, d2
của AB, AC mà AB ⊥ AC nên B, M, C thẳng hàng (bài tập 55)
Vì MA = MB (M thuộc đường trung trực của AB)
MA = MC (M thuộc đường trung trực của AC)
=> MB = MC
Do B, M, C thẳng hàng và M cách đều BC nên M là trung điểm của BC
b) M là trung điểm Bc => MB = 1212 BC
mà AM = MB nên MA =1212 BC
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền
5 tháng 8 2017
a) Giả sử ∆ABC vuông góc tại A. Vẽ hai đường trung trực của hai cạnh góc vuông AB, AC cắt nhau tại M. Ta chứng minh M là trung điểm của BC.
Vì M là giao điểm hai đường trung trực d1, d2
của AB, AC mà AB ⊥ AC nên B, M, C thẳng hàng (bài tập 55)
Vì MA = MB (M thuộc đường trung trực của AB)
MA = MC (M thuộc đường trung trực của AC)
=> MB = MC
Do B, M, C thẳng hàng và M cách đều BC nên M là trung điểm của BC
b) M là trung điểm Bc => MB = BC
mà AM = MB nên MA = BC
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.
CM
26 tháng 12 2017
Xét hai tam giác vuông DAC và DBA ,ta có:
∠ (ADC) = ∠ (BDA) = 90 0
∠ C = ∠ (DAB) (hai góc cùng phụ ∠ B )
Suy ra: △ DAC đồng dạng △ DBA (g.g)
Suy ra: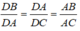 
⇒ D A 2 = D B . D C
hay DA = D B . D C = 9 . 16 = 12 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABD, ta có:
A B 2 = D A 2 + D B 2 = 9 2 + 12 2 = 225 ⇒ AB =15 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ACD,ta có:
AC2 = DA2 + DC2 = 122 +162 = 400 ⇒ AC = 20cm
Vậy BC = BD + DC = 9 + 16 = 25(cm)
30 tháng 5 2017
\(AB^2 + AC^2 = 25^2 = 625\)
\(AD^2 + 81 = AB^2\)
\(AD^2 + 256 = AC^2\)
\(=> AD^2 + 81 + AD^2 + 256 = 625\)
=> \(2AD^2 = 288\)
=> \(AD^2 = 144\)
=> AD = 12(cm)
=>\( AB^2 = 9^2 + 12^2 = 225\)
=> AB = 15 (cm)
=> \(AC^2 = 12^2 + 16^2 = 400\)
=> AC = 20(cm)
và BC = 25(cm)
27 tháng 5 2017
Ta có: \(BC=BD+DC=9+16=25\left(cm\right)\)
Xét \(\Delta DBA\) và \(\Delta ABC\):
\(\widehat{A}=\widehat{D}\left(=90^o\right)\)
\(\widehat{B}=\widehat{A_2}\)(cùng phụ với góc\(A_1\))
\(\Rightarrow\Delta DBA\)~\(\Delta ABC\)
\(\Rightarrow\dfrac{DB}{AB}=\dfrac{AB}{BC}\Leftrightarrow AB^2=DB.BC=9.25=225\Rightarrow AB=15\left(cm\right)\)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC, có:
\(AB^2+AC^2=BC^2\Leftrightarrow15^2+AC^2=25^2\Rightarrow AC=\sqrt{25^2-15^2}=20\)
Vậy các cạnh của tam giác vuông ABC lần lượt là: \(15;20;25\)
CM
17 tháng 5 2018
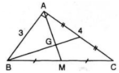
ΔABC vuông tại A có BC2 = AB2 + AC2 (định lí Pitago)
⇒ BC2 = 32 + 42 = 25 ⇒ BC = 5 (cm)
Gọi M là trung điểm của BC ⇒ AM là trung tuyến.
Vì theo đề bài: trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên
